Кинематика движения материальной точки. Динамика вращательного движения твердого тела. Закон сохранения энергии, страница 3

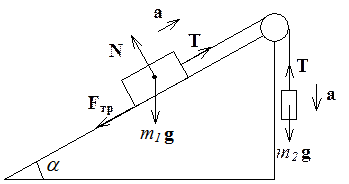
ЗАДАЧА 1. Наклонная плоскость составляет угол a  с горизонтом. Отношение масс тел m₂/m₁=h. Коэффициент трения между телом m₁ и плоскостью m. Массы блока и нитей пренебрежимо малы. Найти модуль и направление ускорения тела m₂, если система пришла в движение из состояния покоя.

РЕШЕНИЕ. Для решения задачи необходимо расставить все силы, действующие на тела m₁ и m₂. Запишем 2-ой закон Ньютона для тел m₁ и m₂, учитывая, что они движутся с одинаковыми ускорениями, т.к. связаны нитью:

     (*)

.

Пусть тело m₂ опускается. Запишем уравнения движения тел в проекциях на направления ускорений:

Для определения силы трения  необходимо записать проекцию уравнения (*) на направление, перпендикулярное ускорению: . Тогда

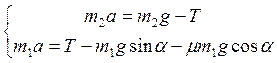
После сложения уравнений получим: . Разделим обе части уравнения на m₁ и  учтем, что m₂/m₁=h:

. Тогда .

ЗАДАЧА 2. На небольшое тело массы m, лежащее на гладкой горизонтальной плоскости, в момент t=0 начала действовать сила, зависящая от времени по закону , где с – постоянная. Направление этой силы все время составляет угол a с горизонтом. Найти скорость тела в момент отрыва от плоскости и путь, пройденный телом к этому моменту.

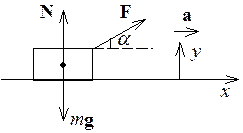РЕШЕНИЕ. По 2-ому закону Ньютона

                                    (*)

В проекции на ось Y: . В момент отрыва от плоскости N=0, поэтому . Отсюда найдем время, когда произошел отрыв тела от плоскости, учитывая, что :

.

Уравнение (*) в проекции на ось X:

.

Поскольку ускорение зависит от времени, нельзя пользоваться формулами равнопеременного движения. Поэтому, исходя из определения  (движение одномерное до отрыва от плоскости), можно найти скорость: 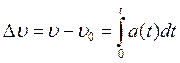. Учтем, что  и найдем скорость тела в зависимости от времени, подставляя ускорение как функцию времени в подынтегральное выражение:

.

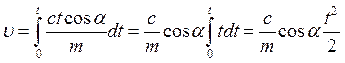Скорость в момент отрыва можно найти, подставив в полученное выражение :

.

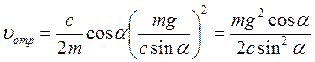По определению , поэтому до момента отрыва тела от плоскости, пройденный телом путь в зависимости от времени можно найти так: .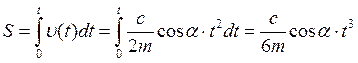

К моменту отрыва от плоскости тело прошло путь:.

ЗАДАЧА 3. Пуля, пробив доску толщиной h, изменила свою скорость от  до . Найти время движения пули в доске, считая силу сопротивления пропорциональной квадрату скорости.

РЕШЕНИЕ. Пусть сила сопротивления , где  - коэффициент пропорциональности. Эта сила сообщает пуле ускорение . По определению в случае одномерного движения , где знак “-” учитывает торможение (т.е. противоположное направление скорости и ускорения).

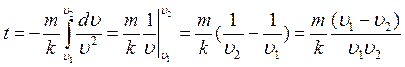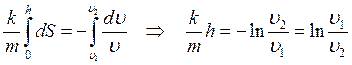После интегрирования последнего уравнения: . Чтобы найти неизвестный коэффициент , перепишем соотношение , учитывая, что . Подставим : . Проинтегрируем: . Отсюда найдем 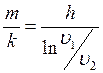. Окончательно: .

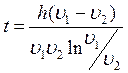ЗАДАЧА 4. Горизонтально расположенный гладкий стержень АВ вращают с постоянной угловой скоростью  вокруг вертикальной оси, проходящей через его конец А. По стержню свободно скользит муфточка массы m, движущаяся из точки А с начальной скоростью . Найти действующую на муфточку силу Кориолиса (в системе отсчета, связанной с вращающимся стержнем) в момент, когда муфточка оказалась на расстоянии r от оси вращения.

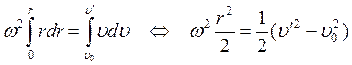РЕШЕНИЕ. Сила Кориолиса , ее величина . Уравнение движения муфточки в неинерциальной системе отсчета, связанной с вращающимся стержнем: . В проекции на ось X, направленную вдоль стержня: . Или, учитывая, что  и , перепишем полученное соотношение: . В этом дифференциальном уравнении легко поделить переменные: . Проинтегрируем: . Отсюда найдем скорость муфточки относительно стержня, когда она находится на расстоянии r от точки А: . Окончательно сила Кориолиса: .

ЗАДАЧА 5. На краю покоящейся тележки массы М стоят два человека, каждый массы m. Пренебрегая трением, найти скорость тележки после того, как оба человека спрыгнут с одной и той же горизонтальной скоростью относительно тележки: 1) одновременно; 2) друг за другом. В каком случае скорость тележки будет больше и во сколько раз?