Динамика системы вещественных точек и дифференциальные уравнения движения твердого тела

Балтийский Государственный Технический Университет

имени Д.Ф. Устинова “Военмех”

Домашнее задание 2

Динамика системы вещественных точек и дифференциальные уравнения движения твердого тела

Преподаватель: Рупасова Н.Е

Студент: Ивкин А.Е

Группа: Н-151

Вариант: 3

Санкт - Петербург

2006

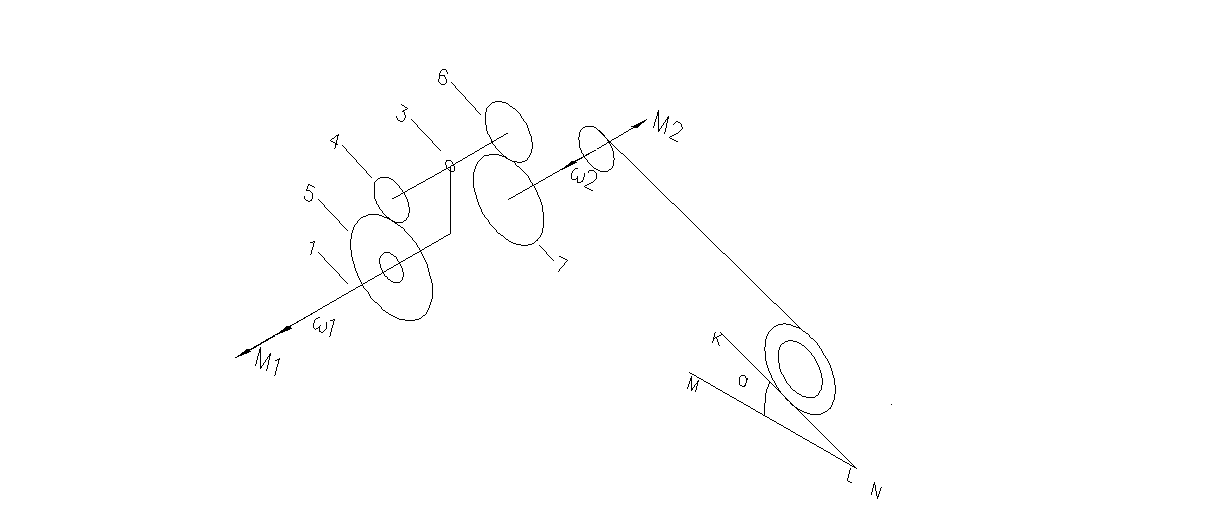
Задание: Для подъема груза вдоль наклонной плоскости KL, образующей угол α с горизонтом MN (Приложение 1) применяется механизм, схема которого изображена на рис. 2.

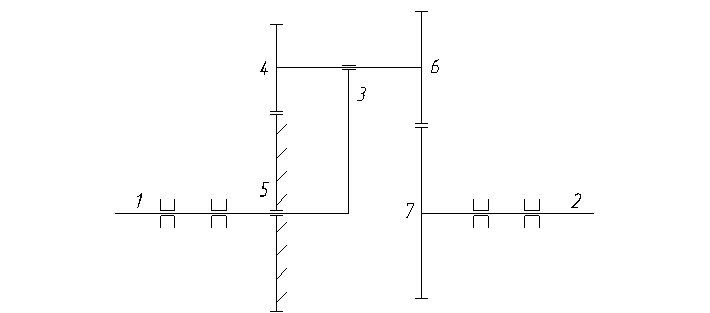
Рис. 2 Схема редуктора

Ведомый вал механизма 2 несет барабан для намотки троса. Ведущий вал механизма связан с ведомым валом с помощью редуктора, представляющего из себя систему шестерен.

К ведущему валу 1 со стороны двигателя приложен постоянный момент М1=1,2М0, где М0 величина момента, приложенного к ведущему валу, необходимого для удержания системы в покое.

Силы сопротивления, приложенные к механизму редуктора условно приведены к моменту М2, приложенному к ведомому валу 2, величина которого пропорциональна угловой скорости вала 2.

Груз катиться по плоскости без проскальзывания. Работой сил тяжести всех движущихся частей редуктора пренебрегаем. Остальные исходные данные сведены в таблицу 1.

Таблица 1. Исходные данные

Вес груза, Н	10Р
Коэффициент сопротивления, α2, Нмс	0,3Ра
Коэффициент трения качения «К»	0,02а
Радиус груза, м	0,6а
Радиус барабана, м	0,3а
Радиус инерции груза ρ, м	0,4а
Угол α, град	20
Радиус шестерни, м:
R3	а
R4	0,3а
R6	0,4a
R7	0,6a
Момент инерции шестерен относительно их осей вращения, кгм^2
I1	2Ра2/3g
I2 (момент инерции вала 2 и барабана)	8Ра2/g
I46	Ра2/2g
Масса шестерни 46, кг	Р/g

1. Определим зависимость угловых скоростей ведомых звеньев механизма редуктора, барабана от угловой скорости вращения ведущего вала 1.

1.1 Найдем скорость относительного движения шестерни 46:

1.2 Угловая скорость шестерни 46 определяется по формуле:

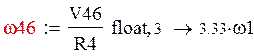
1.3 Найдем скорость относительного движения шестерни 6:

1.4 Угловая скорость шестерни 7 ведомого вала 2 и барабана определяется по формуле:

1.5 Скорость относительного движения шестерни барабана определим по формуле:

1.6 Скорость поступательного движения центра масс груза найдем по формуле:

1.7 Найдем угловую скорость груза:

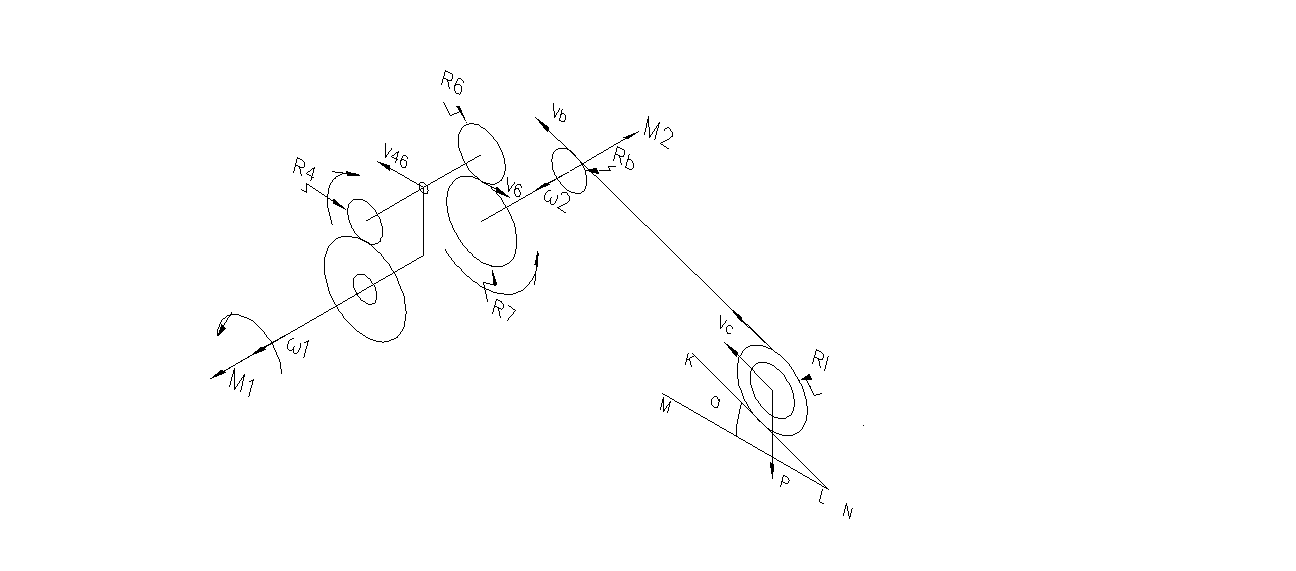
Направления скоростей и угловых скоростей приведены на рисунке в Приложении 2.

2. Найдем кинетическую энергию системы, как сумму энергий каждого тела входящего в эту систему.

где: Т1 - кинетическая энергия ведущего вала редуктора (кинетическая энергия вращательного движения), Т46 – кинетическая энергия шестерни 46 (плоскопараллельное движение), Т2 – кинетическая энергия ведомого вала и барабана (кинетическая энергия вращательного движения), Tload – кинетическая энергия груза, движущегося по наклонной плоскости (плоскопараллельное движение).

где:  Iload – момент инерции груза относительно оси вращения.

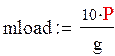
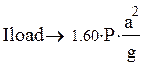
Подставляя значения кинетических энергий в исходную формулу, получаем:

3. Определим элементарную работу всех сил, действующих на систему, выразив ее через элементарное перемещение ведущего вала.

где:

Получаем:

Подставляя значения, получим:

Учитывая что:

Подставляя окончательные результаты, получаем:

4. Найдем величину момента М0 приложенного к ведущему валу 1 и необходимого для удержания системы в покое.

Для этого приравняем элементарную работу всех сил к нолю, следовательно, система неподвижна, а значит и ω1=0.

Получаем значение М0:

Учитывая что вращающий момент, приложенный с валу равен М1=1,2М0 получаем:

Считая, что к ведущему валу приложен момент М1 получаем окончательное значение работы всех сил системы:

5. Запишем кинетическую энергию системы в дифференциальном виде:

Из условия: d’A=dT

получаем следующее:

поделив обе части уравнения на dt, получим следующее уравнение:

учитывая что: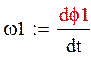

получим:

Записав данное уравнение в конечном виде, получаем дифференциальное уравнение движения ведущего вала 1:

6. Из условия, что в начальный момент времени система была неподвижна найдем зависимость угловой скорости вала 1 от времени, для этого проинтегрируем наше уравнение:

Для упрощения расчета условимся:

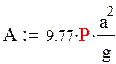
получаем:

интегрируем:

упростив полученное выражение, получаем:

Подставляя значения А, D, B найдем угловую скорость вращения вала 1 как функцию времени:

Примем значения P, a, g следующими:

Построим график зависимости угловой скорости от времени:

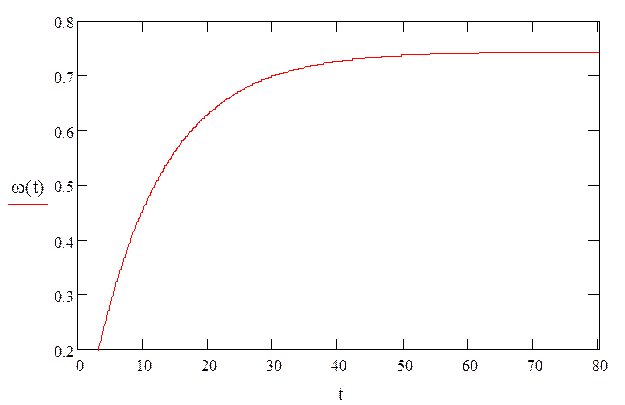
7. Из графика видно что скорость становиться постоянной примерно при 60 секундах и равняется 0,74 рад с^-1