Динамика системы материальных точек.
1. Основные определения. Силы внешние и внутренние.
Системой материальных точек называют совокупность таких точек, движения которых взаимосвязаны.
Массой системы материальных точек называется сумма масс всех точек
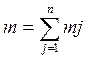 , где n – число
точек в системе, mj – масса j-ой
точки системы.
, где n – число
точек в системе, mj – масса j-ой
точки системы.
При изучении движения системы материальных точек, различают силы внешние и внутренние, действующие на точки системы.
Внешними называются силы, действующие на какую-либо материальную
точку механической системы со стороны тел, не принадлежащих рассматриваемой
механической системе - ![]() .
.
Внутренними называются силы, действующие на какую-либо
материальную точку механической системы со стороны других материальных точек,
принадлежащих рассматриваемой механической системе - ![]() .
.
Свойства внутренних сил.
Как следует из третьего начала динамики – начала взаимодействия – внутренних сил всегда четное число, каждая пара сил имеет общую линию действия, силы равны по модулю и направлены в противоположные стороны. Следовательно, легко показать, что главный вектор и главный момент всех внутренних сил относительно любой точки О равны нулю.
Действительно, возьмем две любые точки M1
и M2. Приложенные к ним внутренние
силы обозначим ![]() и
и![]() .
Выбирая произвольную точку О строим главный вектор этих двух сил:
.
Выбирая произвольную точку О строим главный вектор этих двух сил:
![]()
Так как ![]() , то
, то ![]() = 0
= 0
Строим главный момент этих двух сил относительно (.)О:
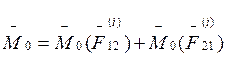 . Но
. Но ![]()
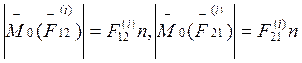 . Так как
. Так как ![]() , то
, то ![]()
Применяя аналогичные рассуждения для каждой другой пары внутренних сил, докажем сформулированное выше утверждение.
Дифференциальные уравнения движения системы.
Пусть система n материальных
точек, массы которых m1, m2,
…mn движется
относительно выбранной системы отсчета и находится под действием сил ![]() (где
(где ![]() -
равнодействующая приложенных к точке
-
равнодействующая приложенных к точке ![]() сил в рассматриваемой
системе отсчета).
сил в рассматриваемой
системе отсчета).
Определить движение системы это значит иметь возможность установить
положение каждой точки системы в любой момент времени относительно выбранной
системы отсчета, то есть определить ![]() .
.
Для каждой точки системы запишем основное уравнение динамики точки (2-ой закон Ньютона).
![]() (1)
(1)
Но
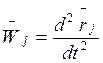 , а
, а ![]()
Поэтому (1) можно записать иначе:
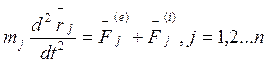 (2)
(2)
Это - векторные уравнения движения.
В проекциях на неподвижные оси декартовых координат:
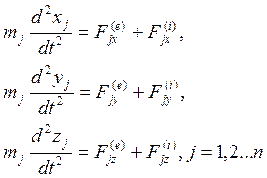 (3)
(3)
Получили 3n динамического уравнения второго порядка. Это динамическое уравнения движения точек системы.
Решение этих уравнений будет содержать 6n произвольных постоянных, которые определяются из начальных условий. Пусть при t=0 известны:
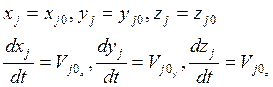 (4)
(4)
Тогда в результате интегрирования уравнений (3) с учетом начальных условий (4) можно получить уравнения движения, то есть
![]() (5)
(5)
О трудностях интегрирования системы уравнений (3).
Теоретически задача о движении системы материальных точек решается выше изложенным способом. Но практически этот способ реализуем по следующим причинам:
1)
Обычно ![]() неизвестны и нет способов их
аналитического выражения, что требуется в уравнениях (3).
неизвестны и нет способов их
аналитического выражения, что требуется в уравнениях (3).
2) Для большого числа n точек системы составление 3n динамического уравнения является громоздкой процедурой.
Эти трудности можно обойти, используя некоторые другие понятия теоретической механики, являющиеся мерами движения: количество движения, кинетический момент, кинетическая энергия системы.
Центр масс механической системы.
Механическая система, состоящая из n материальных точек, движется относительно осей координат 0xyz, неизменно связанных с системой отсчета. Массы точек
системы ![]() , а их положения относительно осей 0xyz определяются в момент времени t радиусами-векторами
, а их положения относительно осей 0xyz определяются в момент времени t радиусами-векторами ![]() или координатами
или координатами ![]() .
.
Центром масс системы материальной точки называется точка, положение которой в рассматриваемый момент времени определяется равенством:
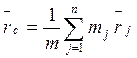 , (1)
, (1)
где m – масса данной системы материальной точки.
Центр масс – геометрическая точка.
Проектируя (1) на оси 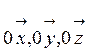 , получим формулы,
определяющие координаты центра массы:
, получим формулы,
определяющие координаты центра массы:
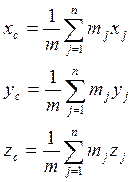 (2)
(2)
Векторное и дифференциальные уравнения движения центра масс.
Пусть движение системы материальной точки происходит под действием
системы сил (![]() ). (1) перепишем в виде
). (1) перепишем в виде 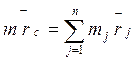 и дважды продифференцируем по времени:
и дважды продифференцируем по времени:
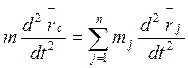 (*)
(*)
Известно, что 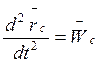 и
и 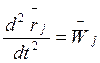
Рассмотрим правую часть (*): 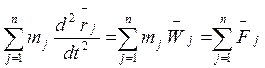 , так как
, так как ![]() , где
, где ![]() -
равнодействующая всех сил, приложенных к j-ой
материальной точки.
-
равнодействующая всех сил, приложенных к j-ой
материальной точки.
Но ![]() . То есть
. То есть 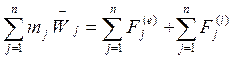
Подставляя в (*), получим: 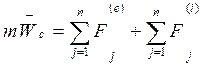 .
.
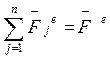 - главный вектор внешних сил;
- главный вектор внешних сил; 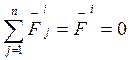 - главный вектор внутренних сил.
- главный вектор внутренних сил.
Окончательно: ![]() (3) – векторное уравнение
движение центра масс системы.
(3) – векторное уравнение
движение центра масс системы.
Центр масс системы материальной точки движется так, как движется материальная точка, в которой сосредоточена масса всей системы и в которой приложены все внешние силы, действующие на систему.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.