Третий закон Ньютона – равенство действия и противодействия двух материальных точек

3. Третий закон Ньютона – равенство действия и противодействия двух материальных точек.

Силы взаимодействия двух материальных точек всегда действуют по одной прямой, противоположно направлены и численно равны между собой.

К m₁ со стороны m₂ приложена сила . На m₂ со стороны действует сила .

Первый и второй законы только для инерциальных систем координат, третий – для любой системы координат, так как в нем нет кинематических характеристик движения.

 и  приложены к разным числам, они неуравновешенны; они уравновешены только в случае абсолютно твердого тела.

4. Четвертая аксиома динамики – о независимости действия сил.

Ускорение , которое получает точка при одновременном действии нескольких сил, равно геометрической сумме ускорений, которые получила бы точка при независимом действии каждой силы.

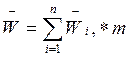
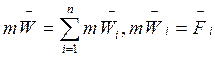
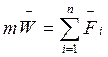
Эти законы – обобщение практических знаний.

Динамическое уравнение движения материальной точки.

Основное уравнение динамики:

1.  Векторный способ.

Известно: 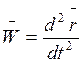 то есть (*) запишется в виде  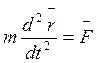- динамическое уравнение в векторной форме.

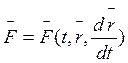 - сила, приложенная к точке, или равнодействующая нескольких сил.

Позиционные силы – зависящие от положения. Сопротивления зависят от скорости. Силы, зависящие от ускорения, в механике не встречаются. Например, силы присоединения масс воды; силы – в вопросах управления.

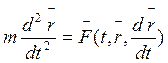- динамическое уравнение движения материальной точки в векторной форме.

2.  Координационный способ.

Спроецируем (*) на неподвижные оси декартовых координат:

 

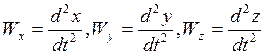
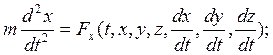
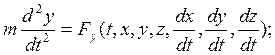
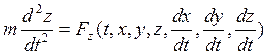
- динамические уравнения движения в координатной форме.

3. Естественный способ.

Спроецируем (*) на оси естественного трехгранника

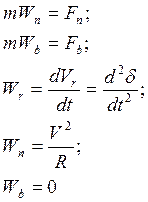
Следовательно, сила , под действием которой движется материальная точка, лежит в соприкасающейся к траектории точки плоскости.

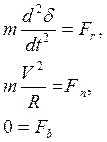е

Две задачи динамики точки.

1.  Прямая задача.

Известны m и движение точки. - силу, действующую на точку (или равнодействующую).

Пусть - кинематические уравнения.

Продифференцируем 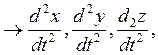 находим  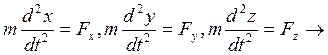модуль силы: алгебраические величины проекций искомой силы на выбранные оси координат.

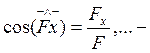направляющие cos-углов, образуемых силой с осями координат.

Эта задача решается всегда, так как операция дифференцирования всегда выполнима.

2.  Обратная задача.

Известны: m и  Определить движение точки под действием заданной силы.

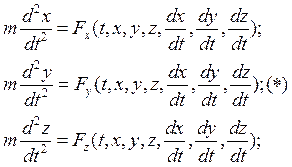
Силы – сложные функции, задача интегрирования намного сложнее. Способ интегрирования – в зависимости от вида функций , , . Система обыкновенная, шестого порядка.

Для однозначного нахождения x, y, z нужно знать:

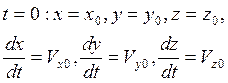 - начальные условия движения.

Это задача Коши. Решая, получим:

(**)

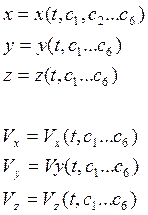Для нахождения Const подставляем начальные условия, их подставляем в общее решение (**). Получаем решение задачи, соответствующее данным начальных условий:

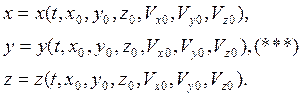
В математике доказывается, что при определенных условиях, накладываемых на правые части динамических уравнений (*) (если задача механики поставлена правильно, они обычно выполняются), решение (***) – единственное. То есть при данных начальных условиях и данных силах движение точки полностью и единственным образом определено.

дставляем начальные условия, их подставляем в общее решение ()сегда выполнима.раектории точки плосткости. при независимом дейс