Кинетический момент системы материальных точек (главный момент количества движения системы материальных точек) относительно неподвижного полюса.
В момент t: количества движения точек ![]()
Кинетическим моментом системы материальных точек относительно полюса О называется геометрическая сумма моментов количеств движения всех точек данной системы относительно того же полюса. Для момента времени t:
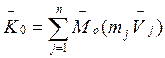 (1)
(1)
Из определения следует, что ![]() имеет начало в (.) О, и
при движении механической системы изменяется и по величине и по направлению.
Раскладывая на составляющие по осям
имеет начало в (.) О, и
при движении механической системы изменяется и по величине и по направлению.
Раскладывая на составляющие по осям ![]() каждый из векторов равенства
(1), получим:
каждый из векторов равенства
(1), получим:
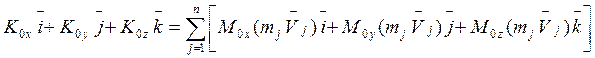 , откуда
, откуда
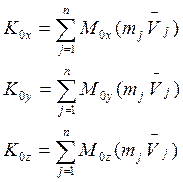 (2)
(2)
(2) – алгебраические величины проекций кинетического момента относительно
полюса О на оси координат ![]() или алгебраические
величины кинетического момента системы относительно осей
или алгебраические
величины кинетического момента системы относительно осей ![]() .
.
Так как ![]() то
то 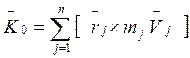 .
.
Так как 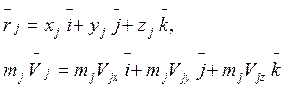
то 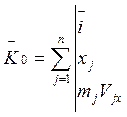
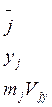
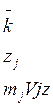
![]() , то есть (2) примут вид:
, то есть (2) примут вид: 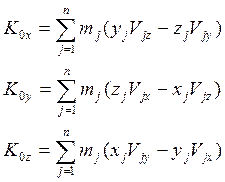
Введем в рассмотрение промежуточную систему координат ![]() , имеющую начало в центре масс механической
системы и оси, параллельной осям системы 0xyz во все время движения системы материальных точек. Движение
механической системы относительно неподвижной системы координат 0xyz (а значит, и каждой ее точки) можно рассматривать
, имеющую начало в центре масс механической
системы и оси, параллельной осям системы 0xyz во все время движения системы материальных точек. Движение
механической системы относительно неподвижной системы координат 0xyz (а значит, и каждой ее точки) можно рассматривать
Переносным движение является движение неизменяемой среды, неизменно связанной с промежуточной системой координат, относительно неподвижной системы 0xyz. Оно является поступательным (оси систем параллельны).
Скорость любой материальной точки относительно осей 0xyz:
![]() , то есть
, то есть
![]() где
где 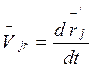 .
.
Переносное движение – поступательное, то есть в один и тот же момент
времени t все точки данной
системы будут иметь в переносном движении одинаковые по величине и направлению
скорости ![]() , определяемые скоростью центра масс С.
механической системы.
, определяемые скоростью центра масс С.
механической системы.
Кинетический момент:
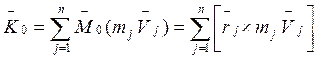 , но
, но ![]() , то
есть
, то
есть
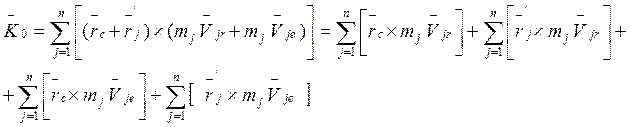 (3)
(3)
В (3) рассмотрим по отдельности каждую сумму:
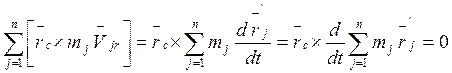 , так как
, так как 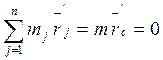 , ибо
в системе координат
, ибо
в системе координат ![]() - начало
- начало ![]() .
.
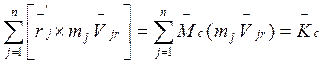 - кинетический момент системы материальных
точек в ее относительном движении.
- кинетический момент системы материальных
точек в ее относительном движении.
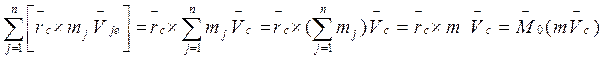 - момент количества движения относительно
полюса 0 материальной точки, имеющей массу данной системы и совпадающей с ее
центром масс.
- момент количества движения относительно
полюса 0 материальной точки, имеющей массу данной системы и совпадающей с ее
центром масс.
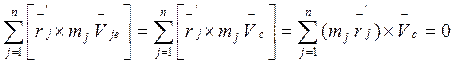 , так как
, так как 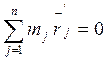
Подставляя найденные значения сумм в (3), получим:
![]() (4)
(4)
Кинетический момент системы материальных точек относительно неподвижного полюса О равен геометрической сумме момента относительно того же полюса количества движения материальной точки, имеющей массу данной системы и совпадающей с ее центром масс и кинетического момента системы относительно центра масс системы в ее движении относительно осей координат, имеющих начало в этом центре и параллельных осям неподвижной системы координат.
Теорема об изменении кинетического момента системы материальных точек относительно неподвижного полюса.
Система материальных точек движется под действием сил ![]() . Для каждой точки уравнение момента
количеств движения:
. Для каждой точки уравнение момента
количеств движения:
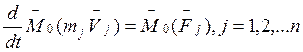 , но
, но ![]() , то
есть
, то
есть ![]() и
и 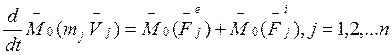
Эти n векторных равенств сложим почленно:
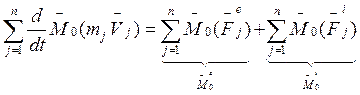 (5)
(5)
![]() - главный момент всех внешних сил,
действующих на систему, относительно полюса О;
- главный момент всех внешних сил,
действующих на систему, относительно полюса О; ![]() -
главный момент всех внутренних сил, действующих на систему.
-
главный момент всех внутренних сил, действующих на систему. ![]() . Значит:
. Значит:
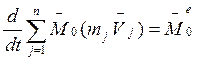 или
или 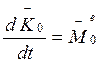 (6)
(6)
Производная по времени от кинетического момента системы материальных точек относительно неподвижного полюса в каждый данный момент времени равна главному моменту относительно того же полюса всех внешних сил, действующих на механическую систему.
(6) спроецируем на оси ![]() :
:
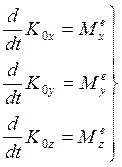 (7), где
(7), где 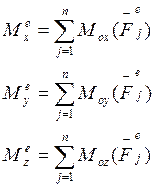
(7) – уравнения кинетического момента системы материальных точек относительно осей.
Частные случаи.
1.
Закон сохранения кинетического момента системы материальных точек
относительно неподвижного полюса. Если система сил (![]() )
действующих на систему материальных точек такова, что
)
действующих на систему материальных точек такова, что ![]() ,
то
,
то
![]() (8)
(8)
Если главный момент внешних сил относительно неподвижного полюса равен нулю, то кинетический момент системы материальных точек относительно того же полюса во все время движения системы остается постоянным по величине и направлению, равным его значению в начальный момент времени.
2.
Закон сохранения кинетического момента системы материальных точек
относительно оси. Если система такова, что 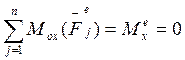 , то
, то ![]() .
.
Уравнения кинетического момента системы материальных точек относительно ее центра масс.
Если в качестве подвижного полюса принять центр масс системы, то уравнение (6) запишется так же как если бы (.)С была неподвижной, то есть
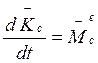 (9)
(9)
Докажем, что (9) выполняется в любой момент времени.
Из (4): 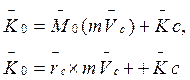 ;
;
левая часть (6): 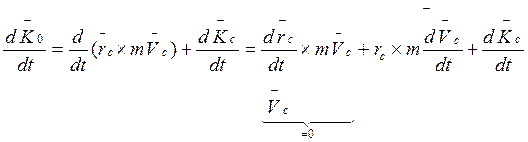 ;
;
правая часть (6): 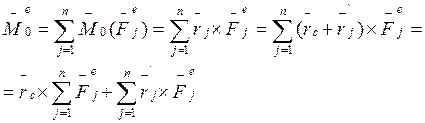 .
.
Приравняем:
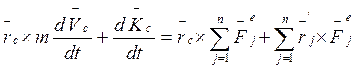 (10)
(10)
- в (10) уничтожаются, так как из векторного уравнения движения центра масс.
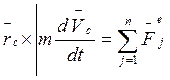
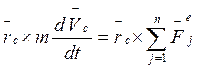 и (9) доказано.
и (9) доказано.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.