Из (3) следует, что внутренние силы не влияют на движение центра масс.
Движение автомобиля возможно при наличии силы трения ![]() между
задним (ведущим) колесом автомобиля и дорогой. Она не может возникнуть без
внутренних, передающих вращающий момент на ведущие колеса. Если выключить
двигатель, то
между
задним (ведущим) колесом автомобиля и дорогой. Она не может возникнуть без
внутренних, передающих вращающий момент на ведущие колеса. Если выключить
двигатель, то ![]() обратятся в нуль, автомобиль
остановится. Спроецируем (3) на оси
обратятся в нуль, автомобиль
остановится. Спроецируем (3) на оси ![]() :
:
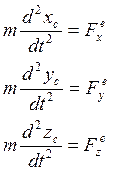 (4)
(4) 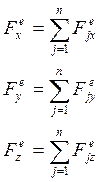
(4) – динамическое уравнение движения центра масс системы материальной точки. Система (4) имеет 6 порядок. Для интегрирования нужно задать 6 н.у.
При t=0: 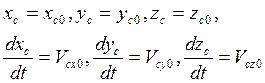
Главный вектор внешних сил – сложная функция координат и скоростей точек системы. Интегрирование (4) – сложная и не всегда разрешимая задача.
Частные случаи.
1. Закон сохранения движения центра масс.
Если главный вектор внешних сил равен нулю ![]() , т о из
(3) следует, что
, т о из
(3) следует, что ![]() , то есть
, то есть ![]() (5)
(5)
Если главный вектор внешних сил, действующих на систему материальных
точек, равен нулю, то центр масс этой системы будет двигаться равномерно и
прямолинейно ( если ![]() ) или будет неподвижным (если
) или будет неподвижным (если ![]() ) относительно выбранной системы отсчета.
) относительно выбранной системы отсчета.
Если  , то из (4) следует
, то из (4) следует  ,
то есть
,
то есть 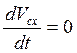
То есть ![]() - центр масс системы движется
равномерно вдоль оси
- центр масс системы движется
равномерно вдоль оси ![]() (если
(если ![]() )
или неподвижен относительно этой оси (если
)
или неподвижен относительно этой оси (если ![]() ).
).
2. Закон сохранения положения центра масс.
Если главный вектор внешних сил ![]() и
начальная скорость центра масс
и
начальная скорость центра масс ![]() , то из (5) следует, что
в любой момент времени скорость центра масс механической системы
, то из (5) следует, что
в любой момент времени скорость центра масс механической системы ![]() . То есть положение центра масс
относительно выбранной системы не будет изменяться, то есть
. То есть положение центра масс
относительно выбранной системы не будет изменяться, то есть
![]() (6)
(6)
Если ![]()
![]() значит
значит ![]() и следовательно,
и следовательно, ![]()
Замечание.
В разделе «Статика» было введено понятие центра тяжести твердого тела. Для системы материальной точки положение центра тяжести определяется:
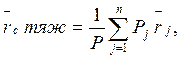
где 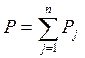 - все системы.
- все системы.
Центр масс и центр тяжести – разные точки или они геометрически совпадают?
Если система занимает относительно Земли незначительное пространство, то
для всех точек ее ![]() ускорение свободного падения
ускорение свободного падения ![]() - одинаково.
- одинаково.
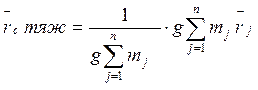
- центр масс и центр тяжести совпадают.
Понятие центра масс более широкое, так как при его введении не было сделано никаких ограничений для системы материальной точки.
Понятие центра тяжести требует, чтобы система материальной точки обязательно находилась в поле силы тяжести.
Теорема об изменении количества движения системы материальных точек.
Количество движения системы материальных точек.
Количеством движения системы материальных точек называется вектор ![]() , равный сумме количеств движения точек,
входящих в систему:
, равный сумме количеств движения точек,
входящих в систему:
 (1)
(1)
Количеством движения системы материальной точки по направлению какой-либо оси называется сумма количеств движений всех точек данной системы по направлению указанной оси в рассматриваемый момент времени.

Так как 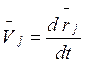 , где
, где ![]() -
радиус-вектор j-ой точки, проведенный из начала
инерциальной системы отсчета 0xyz. Подставляя в формулу
(1) и меняя местами дифференцирование и суммирование (можно, так как n=Const)
-
радиус-вектор j-ой точки, проведенный из начала
инерциальной системы отсчета 0xyz. Подставляя в формулу
(1) и меняя местами дифференцирование и суммирование (можно, так как n=Const)
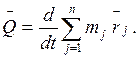
Но 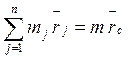 , где m – масса
системы материальных точек,
, где m – масса
системы материальных точек, ![]() - радиус-вектор центра
масс. То есть
- радиус-вектор центра
масс. То есть 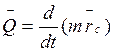 ,
, 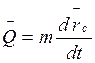 .
.
Так как 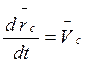 - скорость центра масс системы,
то есть
- скорость центра масс системы,
то есть
![]() (2)
(2)
Количество движения системы материальных точек равно количеству движения ее центра масс, если сосредоточить в нем массу всей системы.
Теорема об изменении количества движения системы материальных сил.
Запишем векторные уравнения движения точек системы материальных точек:
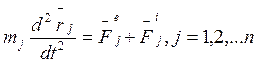
Сложим почленно все уравнения:

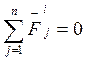
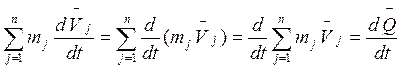
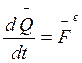 (3)
(3)
Производная по времени вектора количества движения системы материальных точек равна главному вектору всех внешних сил, действующих на систему.
В проекциях на неподвижные оси декартовых координат:
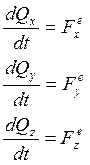
Умножим обе части (3) на dt и проинтегрируем в пределах от 0 до t.
(4) 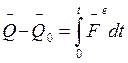 ,
,
теорема об изменении количества движения системы материальных точек в
интегральной форме, где ![]() - количество движения
системы материальных точек в момент времени t,
- количество движения
системы материальных точек в момент времени t, ![]() - в нулевой момент времени.
- в нулевой момент времени.
Изменение количества движения системы материальных точек за некоторый промежуток времени равно импульсу главного вектора внешних сил, приложенных к системе за тот же промежуток времени. (4) широко применяется в теории удара.
Следствия:
1. Внутренние силы системы не могут изменить количества движения системы.
2а. Если главный вектор внешних сил, приложенных к системе равен нулю в
течение рассматриваемого промежутка времени, то количество движения системы не
изменится за рассматриваемый промежуток времени, то есть если ![]() или
или ![]() .
.
2б. Если равна нулю проекция главного вектора внешних сил на какую-либо
ось в течение некоторого промежутка времени, то неизменным остается количество
движения системы в направлении этой же оси за тот де промежуток времени, то
есть если ![]() или
или ![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.