Корабельная система координат Крылова А.Н.

Качка корабля на волнении,

Корабельная система координат Крылова А.Н.

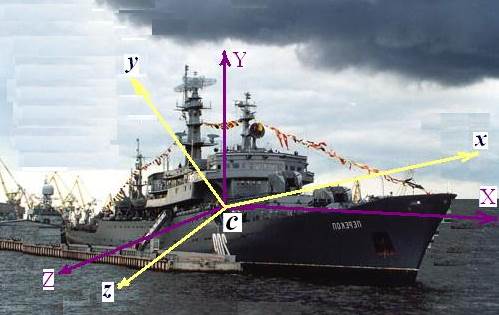
Углы Крылова

угол дифферента , (килевая качка)

угол  крена , (бортовая качка)

угол рыскания .

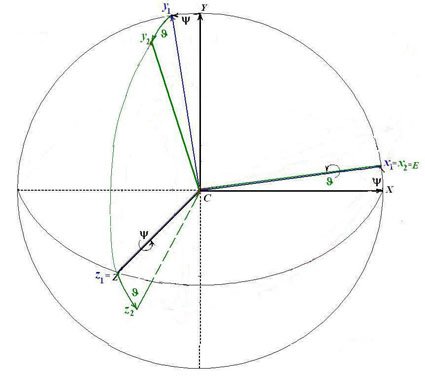
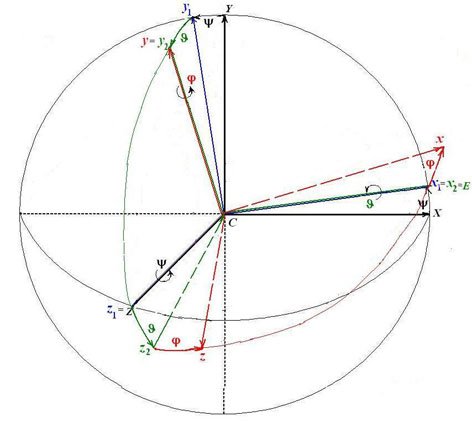
Переход от осей неподвижной системы координат CXYZ к системе Cxyz, неизменно связанной с кораблем, выполняется с помощью трех поворотов:

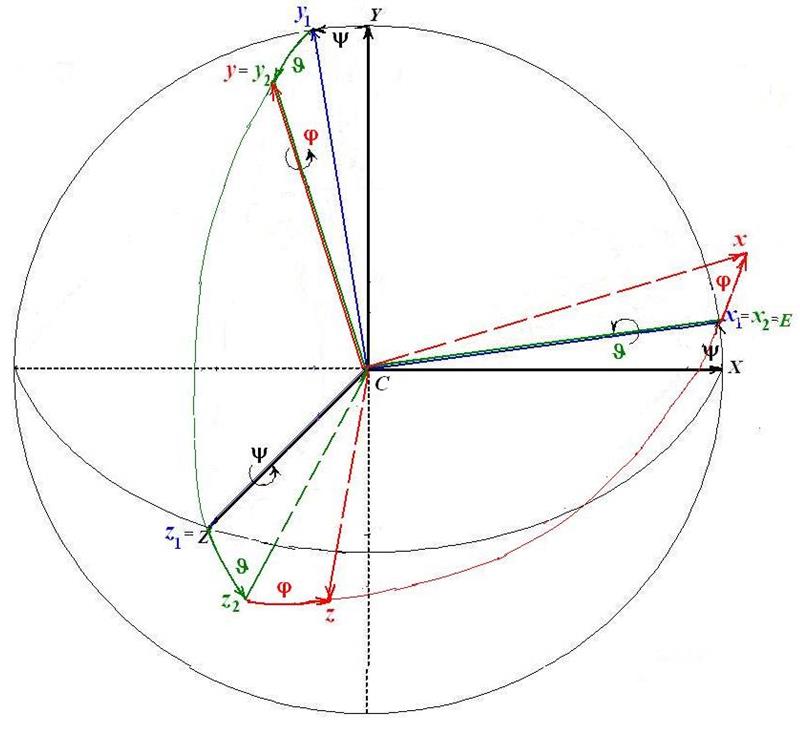
1) поворот системы CXYZвокруг третьей из координатных осей CZ= Cz₁  на угол дифферента , в результате чего получим  систему Cx₁y₁z_1.

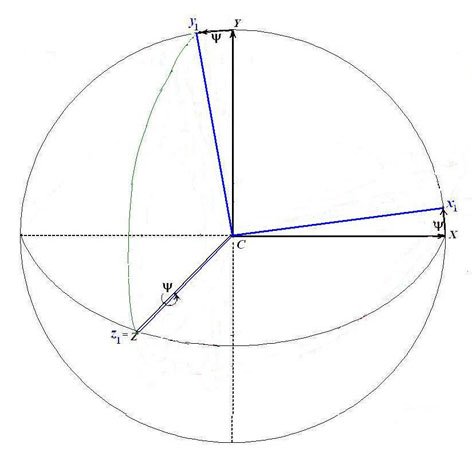
Формулы преобразования координат связаны следующими соотношениями в матричной форме:

от CXYZ Þ к  [X] ={ a_3y}^т [x₁] ,   

или 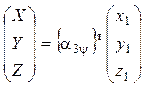  (1) , где  - поворотная матрица, транспонированная к матрице,

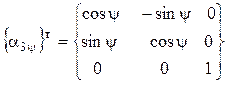  . (2).

2) поворот системы  вокруг первой из координатных осей  на угол крена , в результате чего получим систему ,  при этом  .

Формулы преобразования координат связаны следующими соотношениями в матричной форме:

от системы   Þк системе    

[x₁] =  [x₂] , или 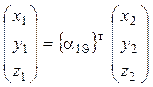(3),  где  – поворотная матрица, транспонированная к матрице ,

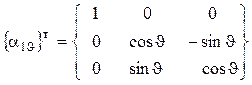. (4)

3) поворот системы  вокруг второй из координатных осей  на  угол рыскания , в результате чего приходим  к системе Cxyz, при этом. = .

Формулы преобразования координат связаны следующими соотношениями в матричной форме:

от системы координат Þ  к системе Cxyz[x₂]= [x],  или 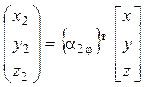,(5) где поворотная матрица {a_2j }^т – это матрица, транспонированная к матрице { a_2j }, имеет вид

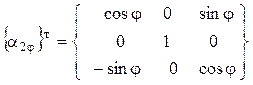 (6).                                           (6)

Подставляя в  (1) соотношения (3) и  (5), получаем:

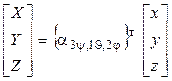 или    или  , (7)

Где матрица  транспонирована к матрице направляющих косинусов , является произведением трех поворотных матриц

 =

=

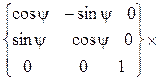
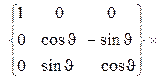
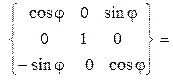
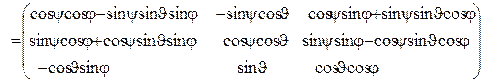.(8)