Кинематика точки. Кинематика твердого тела. Кинематика сложения движений

1.  Краткие сведения из теории

1.1. Кинематика точки

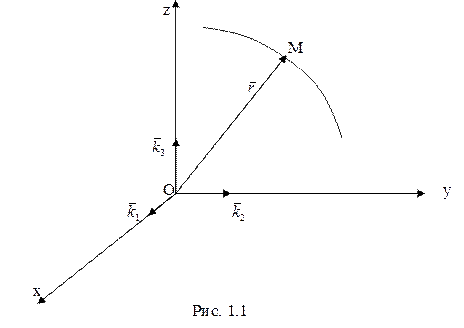
Движение точки может быть задано тремя различными способами. Векторный способ состоит в задании радиус-вектора точки (рис.1.1) как функции времени . Так как пространство трехмерно, то положение точки задается тремя ее координатами . Задание зависимостей координат точки от времени определяет координатный способ задания движения точки:

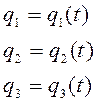                                                                                   (1.1)

Радиус-вектор и координаты точки связаны соотношением

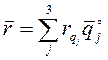,                                                                                (1.2)

где  - орты координатных осей. Если это декартовы координаты (x,y,z), то последняя формула принимает вид

.

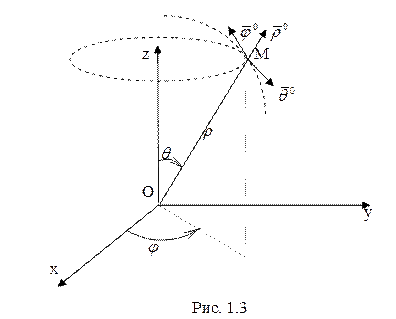
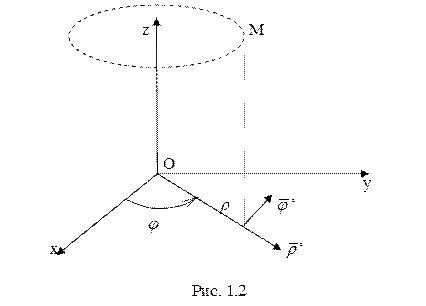Для цилиндрических координат (рис. 1.2) вид формулы (1.2): , для сферических координат  (рис. 1.3): .

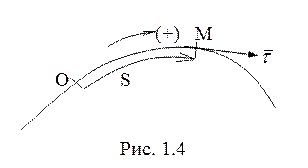          Траекторный способ задания движения точки используется, если траектория точки известна. Начало траекторных координат расположено в одной из точек кривой, на которой лежит траектория, а положение точки характеризуется длиной дуги этой кривой от начала координат до текущего положения точки, взятой с соответствующим знаком в зависимости от положения точки и направления отсчета траекторной координаты (рис. 1.4).

                                                                                     (1.3)

Для перехода от координатного способа задания движения точки к траекторному необходимо найти траекторию и закон движения вдоль нее (1.3). Уравнения (1.1) могут рассматриваться как уравнения траектории точки, заданной в параметрической форме, где роль параметра играет время . Для нахождения явных уравнений кривой, на которой лежит траектория, следует из уравнений (1.1) исключить время, получив соотношения вида

                                                                        (1.4)

Траектория точки может быть всей кривой, задаваемой системой (1.4), или ее частью, в зависимости от вида функций в правой части (1.1) и особенностей движения самой точки (как принадлежащей реально движущейся механической системе).

Если установлена связь декартовых и используемых координат

то зависимость (1.3) получается из следующей формулы:

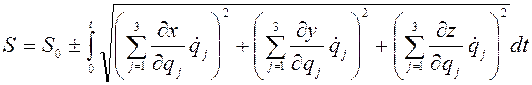, где  - начальная траектория координата, а знак «+» или «-» в формуле выбирается в зависимости от того, в положительном или отрицательном направлении по траектории движется точка.

Скорость точки направлена по касательной к траектории в сторону движения точки. При векторном способе задания движения она вычисляется по формуле ; при координатном:

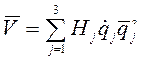,                                                                          (1.5)

где 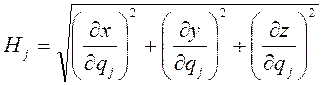 - коэффициенты Ламэ.

В декартовых координатах формула (1.5) принимает вид , в цилиндрических ,в сферических .

При траекторном способе задания движения точки ,  - единичный вектор касательной к траектории (рис. 1.4).

Ускорение точки является производной от скорости по времени . Соответственно при векторном способе задания движения , при координатном в случае ортогональности координат

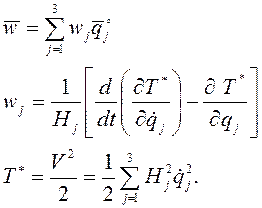
                                                    (1.6)

Из (1.6) следует, что для декартовых координат , для цилиндрических , для сферических

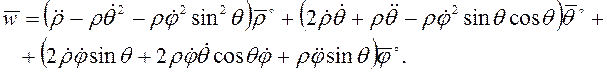
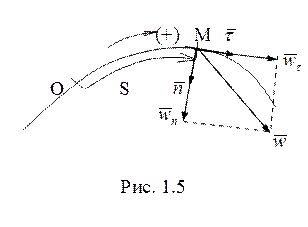При траекторном способе задания движения точки 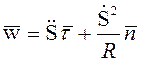, где  – радиус кривизны траектории,  - единичный вектор главной нормали к траектории (рис. 1.5).

Касательное и нормальное ускорения

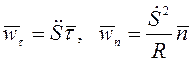
Радиус кривизны траектории может быть вычислен как ,  . Ускорение точки не может быть направлено в сторону выпуклости траектории.

1.2. Кинематика твердого тела

При произвольном движении твердое тело имеет шесть степеней свободы, в частных случаях это число меньше. Общие формулы для скорости и ускорения точек твердого тела имеют вид

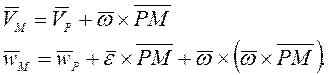                        (1.7)

Здесь  - угловая скорость твердого тела,  - угловое ускорение твердого тела. В качестве полюса Р принимается точка, скорость и ускорение которой известны или без особых трудностей могут быть найдены. Для частных случаев движения твердого тела характеристики этого движения вычисляются следующим образом. Здесь  – неподвижные оси;  - оси, жестко связанные с телом.

(а) Поступательное движение

Тело здесь не меняет своей пространственной ориентации.

Скорости и ускорения всех точек тела в фиксированный момент времени одинаковы. Для задания движения достаточно задать движение одной из точек тела, а следовательно, задача определения характеристик движения здесь эквивалентна задаче кинематики точки.