Кинематика точки. Кинематика твердого тела. Кинематика сложения движений, страница 2

(б) Вращение около неподвижной оси

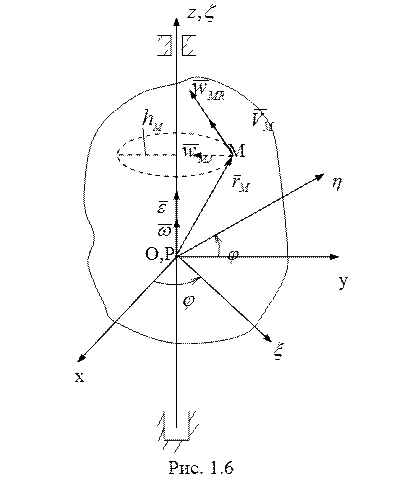
Тело имеет одну степень свободы, и для задания движения достаточно задать зависимость угла поворота от времени  (рис. 1.6).

Угловая скорость и угловое ускорение .

Угловая скорость направлена вдоль оси вращения в ту сторону, откуда кажется, что поворот происходит против часовой стрелки.

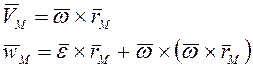
Каждая из точек тела движется по окружности, радиус которой равен  – расстояние от точки до оси вращения. Скорость точки направлена по касательной к этой окружности в сторону движения, .

 - вращательное ускорение (направлено по касательной к указанной окружности), .

  –   осестремительное ускорение (направлено к центру указанной окружности, или по перпендикуляру от точки М к оси вращения),  .

(в) Плоскопараллельное движение

Точки тела здесь движутся в плоскостях, параллельных некоторой неподвижной плоскости. Поэтому достаточно рассмотреть движение не всего тела, а только сечения тела плоскостью, параллельной этой плоскости и проходящей через полюс Р (рис. 1.7). Оси Ox, Oy,  выбраны в этой плоскости, а оси  перпендикулярны ей.

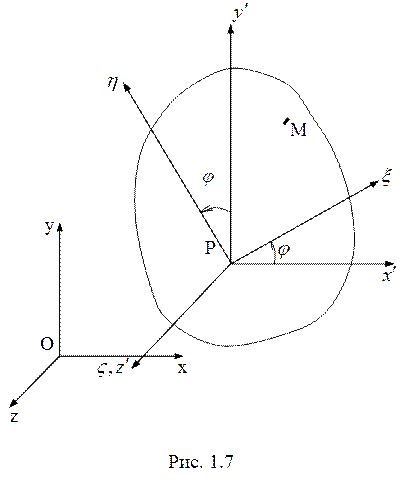Тело имеет три степени свободы, движение задается заданием зависимостей:

Координаты произвольной точки:

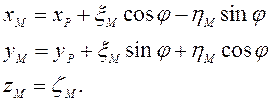
Угловая скорость и угловое ускорение  (перпендикулярны плоскости движения); скорость и ускорения точек

 

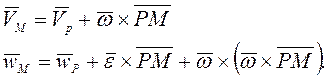
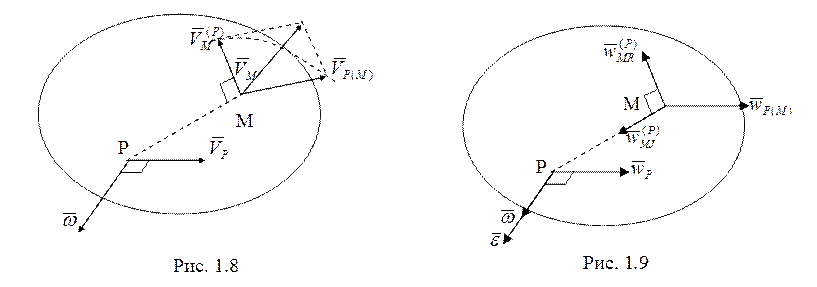
(скорость поворота относительно полюса) (рис. 1.8).

Вращательное ускорение  (рис. 1.9); осестремительное ускорение  (направлено из точки М в полюс Р).

При вычислениях используются не только приведенные формулы, но и особенности движения точек в условиях поставленной задачи.

Точка С плоскости движения полюса Р, связанная с движущимся телом, скорость которой в данный момент времени равна нулю, называется мгновенным центром скоростей. Тогда . Мгновенный центр скоростей не существует, если угловая скорость тела равна нулю. Скорость точек тела

.

Положение мгновенного центра скоростей можно определить при известных направлениях скоростей точек (рис. 1.10).

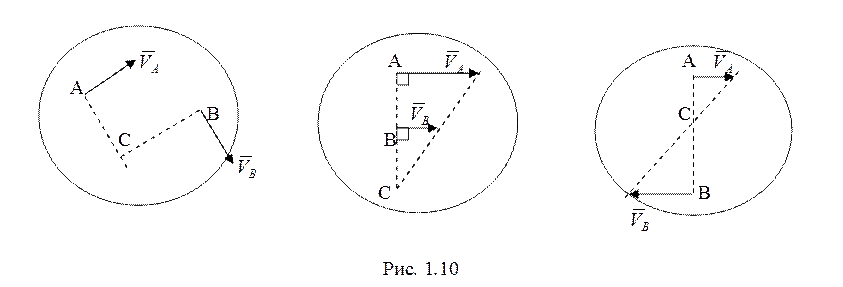При качении тела без проскальзывания по поверхности другого неподвижного тела мгновенный центр скоростей находится в точке соприкосновения тел.

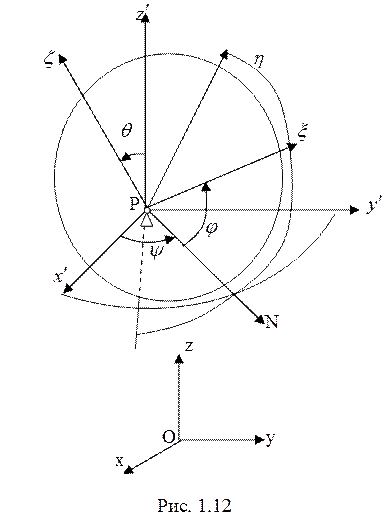
(г) Вращение около неподвижной точки

Тело имеет три степени свободы. Движение задается через задание зависимости от времени трех независимых величин, связанных с углами поворота тела. Если это углы Эйлера  (рис. 1.11), то .

Угловые скорости прецессии, ротации и нутации:

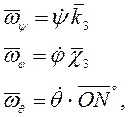
угловая скорость           , угловое ускорение

.

Скорость и ускорение точки

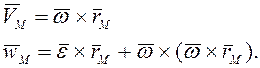
Скорость точек, лежащих на прямой, проходящей через неподвижную точку О вдоль вектора угловой скорости , равна нулю, и эта прямая называется мгновенной осью вращения. Осестремительное ускорение  направлено по перпендикуляру из точки к мгновенной оси вращения. Вращательное ускорение .

При регулярной прецессии ,и .

(д) Общий случай движения

Тело имеет все шесть степеней свободы (рис. 1.12)

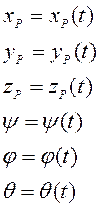
Угловая скорость и угловое ускорение

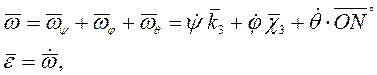
скорость и ускорение точки тела

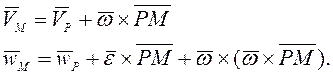
1.3. Кинематика сложения движений

При движении точки относительно подвижной системы отсчета (относительное движение) ее движение относительно неподвижной системы отсчета (абсолютное движение) получается как результат сложения относительного движения и движения вместе с подвижной системой отсчета относительно неподвижной. Подвижная система отсчета часто бывает связана с некоторым твердым телом. Движение воображаемой абсолютно твердой среды, жестко связанной с подвижной системой отсчета, относительно неподвижной системы отсчета, называют переносным движением. Переносным движением точки М является движение той точки указанной среды, положение которой в рассматриваемый момент времени совпадает с положением точки М.

Характеристики движения при этом складываются в соответствии с теоремами сложения. Для скоростей это   ( - абсолютная, относительная и переносная скорости точки – в дальнейшем обозначения индексов, соответствующие трем указанным видам движения, сохраняются); для ускорений , ускорение Кориолиса .

Если сложение движений испытывает твердое тело, то теоремы сложения для его точек те же, а для таких характеристик движения тела в целом, как угловая скорость и угловое ускорение:

,   .

Слагаемые, входящие в приведенные здесь формулы, вычисляются по формулам кинематики точки и твердого тела, а также с учетом особенностей движения рассматриваемой механической системы.