Движение точки относительно двух систем отсчета, перемещающихся одна относительно другой

Балтийский Государственный Технический Университет

имени Д.Ф. Устинова “Военмех”

Домашнее задание 1

Движение точки относительно двух систем отсчета,

перемещающихся одна относительно другой

Преподаватель:

Студент:

Группа: Н- 261

Вариант: 2

Санкт - Петербург

2007

Задание: Пластина «D» вращается вокруг оси Oz неподвижной системы координат Oxyz. Вращение описывается уравнением:

По пластине, по дуге радиуса R, движется точка «М». Траекторная координата этого движения описывается уравнением:

Траекторная координата отсчитывается от точки «Н».

a=0

l=24

r=12cм

k=2

b= - 6π cм/c

c= - 12π cм/c

t1=0.5 c

1. Определим положение точки в соответствующий момент времени:

S(0,5)= -18.84

из этого следует, что в момент времени t=2, заданная точка находится в точке начала отсчета.

2. Определим кинематические величины движения заданной точки относительно системы координат связанной с пластиной.

2.1 Скорость относительного движения точки определяется по формуле:

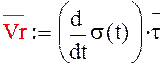
Vr =  - 18 π= - 56.52

Скорость направлена по касательной к траектории движения.

2.2 Ускорение относительного движения точки определяется по формуле:

где:

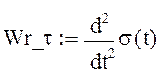
Wr_t= - 24π=-75.36

тангенсальное (касательное) ускорение, направленно по касательной к траектории движения точки.

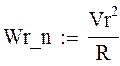
Wr_n = 243 cm/c

нормальное ускорение, направленно по нормали к траектории движения точки.

Wr=254 cm/c

3. Определим кинематические характеристики точки в переносном движении.

3.1 Переносная скорость точки определяется по формуле:

где:

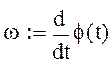
ω=2

угловая скорость вращения пластины относительно неподвижной системы координат.

Ve=48

3.2 Переносное ускорение точки найдем по формуле:

где:

We_oc = 96

осестремительное ускорение точки, направлено к оси вращения пластины.

где:

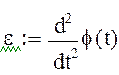
ε =4 

угловое ускорение вращения пластины относительно неподвижной системы координат

We_rot= 96

вращательное ускорение точки, направлено по касательной к траектории движения.

We=135

4. Ускорение Кориолиса определяется по формуле:

Wc= - 226.08

направление определяется правилом векторного произведения (правило правого винта).

5. Определим абсолютное движение заданной точки относительно неподвижной системы координат.

5.1 Абсолютная скорость определяется по формуле:

Va=74,2

5.2 Абсолютное ускорение определяется по формуле:

Wa=336