Впервые механические метод был предложен и применен Н. В. Калакуцким при исследовании остаточных радиальных и тангенциальных напряжений в орудийных стволах [39]. Техника эксперимента состоит в следующем. На торец диска, отрезанного от ствола, наносится несколько концентрических окружностей. Затем диск разрезается на кольца так, чтобы каждое кольцо имело на торце окружность, намеченную вначале. Измерение диаметра этих окружностей до и после разрезки на кольца позволяет установить деформации кольца по диаметру и, следовательно, наличие в диске до разрезки тангенциальных и радиальных напряжений. Найденное значение деформации подставляется в выражение для перемещения в задаче Ляме:
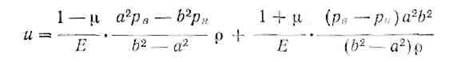
где и— перемещение по радиусу; μ — коэффициент Пуассона; Е— модуль упругости; Ре» Рн— внутреннее и наружное давление; а, Ь-— внутренний и наружный радиусы;
р— расстояние рассматриваемой точки от оси трубы.
После определения по этой формуле внутреннего и наружного давлений рассчитывают радиальные и тангенциальные остаточные напряжения аг и ot по следующим формулам:
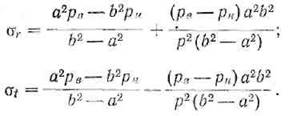
Эти формулы не учитывают наличия осевых остаточных напряжений, так как Н. В. Калакуцкий предполагал, что они отсутствуют. Однако это предположение справедливо лишь в том случае, если высота кольца не превышает 0,2 диаметра.
Метод Н. В. Калакуцкого был развит Н. Н. Давиденковым и X. Гейном [28]. Это развитие выразилось в упрощении техники эксперимента и увеличении точности измерений. Новый эксперимент состоит в следующем. Концентрические кольца вырезаются из диска без предварительного нанесения окружностей. После вырезки измеряются диаметры и ширина колец. Повторное измерение диаметра производится после разрезки кольца по образующей. Найденное значение изменения диаметра Z)b вызванного этой операцией, используется для определения тангенса угла наклона эпюры тангенциальных остаточных напряжений:
![]()
где D — средний диаметр кольца; A£>i — среднее изменение диаметра кольца при разрезке по образующей. Та же величина может быть найдена с использованием изменения расстояния между двумя метками по обе стороны разреза Да:
![]()
Для определения остаточных напряжений в сплошных и полых цилиндрах широкое применение находит способ Г. Закса [109], состоящий в следующем. Цилиндр, в котором надлежит определить распределение остаточных напряжений, подвергается последовательной обточке или расточке, причем толщина снимаемых слоев должна быть по возможности одинаковой на всем протяжении обработки. После снятия каждого слоя точно измеряются диаметр и высота цилиндра.
Напряжения в этом случае определяются по следующим формулам:
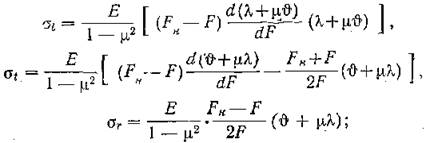
б) при обточке цилиндра
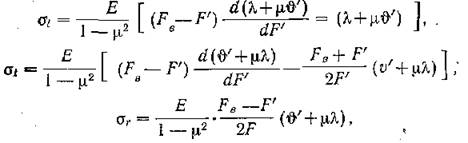
а) при расточкецилиндра где о*/ —осевые остаточные напряжения;
Gt — тангенциальные остаточные напряжения; о> — радиальные остаточные напряжения; Е — модуль упругости; (х — коэффициент Пуассона; F — площадь сечения, соответствующая внутреннему диаметру цилиндра, меняющаяся при расточке; F'— площадь сечения, соответствующая наружному диаметру цилиндра, меняющаяся при обточке; FH, Fe—площади сечения, соответствующие наружному и внутреннему диаметру цилиндра; υ — относительное изменение высоты цилиндра; •&, О'— относительные изменения наружного и внутреннего диаметра цилиндра. Для определения остаточных напряжений в призматических брусьях применима формула Н. Н. Давиденкова, выведенная им для определения осевых остаточных напряжений в полосках, вырезанных из тонкостенных труб [281. Формула имеет вид
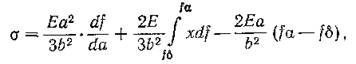
а — расстояние от наружной поверхности до середины рассматриваемого слоя; £ —половина базы (полухорда), на которой измеряется стрела прогиба; δ — начальная толщина бруса;
х текущая координата всех слоев (аналогично а измеряется до ередины слоев).
df *а лс иφ
Величины —- и f xaf находят графически по экспериментальным кривым f = ср(а) и х = ц>ч(а). Техника эксперимента в этом случае состоит в сострагивании слоев с одной стороны бруса и измерении стрелы прогиоа, ооразо-вавшегося в результате этой операции.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.