Остаточные сварочные напряжения и причины их возникновения. Температурный цикл сварки как источник возникновения остаточных напряжений, страница 2

При движении источника тепла изотермы передвигаются с той же скоростью, и различные сечения сварного соединения в разное время проходят через одинаковые температурные состояния. С увеличением скорости движения источника тепла уменьшается протяженность изотермы вдоль шва. Используя теоретические данные, полученные Н. Н. Рыкалипым, можно определить температуры различных точек сварного соединения в зависимости от расстояния до источника тепла и для различных моментов времени.

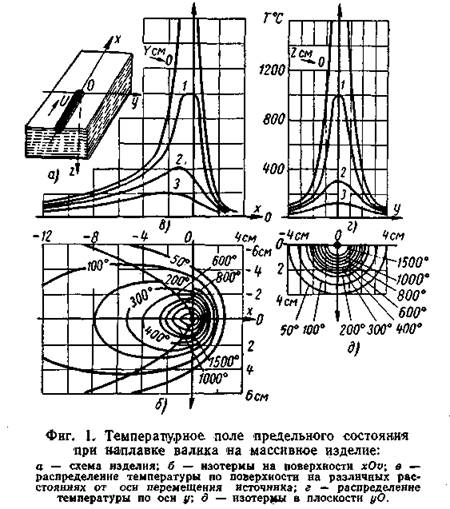
На фиг. 1 показан пример температурного поля предельного состояния (81]. Как видно, это поле обладает очень высоким градиентом температур.

Если при нагреве какого-либо элемента температура по его ширине распределяется равномерно или по линейному закону. то нагрев и остывание не вызовут в нем ни временных напряжений в процессе сварки, ни остаточных напряжений после полного остывания [72]. Если распределение температуры по ширине элемента неравномерно, то вследствие жесткости элемента в процессе нагрева в нем будут возникать временные напряжения. Если эти временные напряжения не превзойдут предела текучести материала (при данном виде напряженного состояния и при данной температуре), то к моменту полного остывания температурные напряжения исчезнут и остаточные напряжения не возникнут. Если же в процессе Нагрева или остывания временные температурные напряжения в какой-либо части сечения элемента достигнут предела текучести и появятся пластические деформации, то после полного остывания в элементе будут существовать остаточные  напряжения.

Для более наглядного представления о механизме возникновения остаточных напряжений в зависимости от температурного цикла нагревания и охлаждения детали используем схему к предложенную В. П. Вологдиным [18]. Если помещенный без зазора между двумя неподвижными и нетеплопроводными стенками цилиндрический элемент (фиг. 2, а) нагревать, то при неизменном расстоянии между стенками увеличится его поперечное сечение. Поскольку удлинение элемента вследствие нагрева стеснено стенками, в нем появятся внутренние напряжения сжатия, величина которых определится формулой Гука:

здесь А/о — приращение длины элемента, которое   он   мог   получить при свободном расширении;

где /о — длина  элемента;

а — коэффициент линейного расширения;

Т — температура нагрева. Подставив значение А10 в формулу для о, получаем

т. е. линейную зависимость, так как величины Е и а — константы материала элемента, на диаграмме а — Т изобразится прямой 0А (фиг. 2, б).

Однако рост напряжений происходит только до тех пор, пока они не достигают значения предела текучести от. Это произойдет при определенной температуре Тв. Если охлаждение элемента начинается до того, как он будет нагрет до этой температуры, напряжения в нем исчезнут, так как они были упругими (если пренебречь явлением гистерезиса), и элемент примет первоначальные размеры (фиг. 2, в). Остаточных явлений в этом случае не наблюдается.

Если же нагревать элемент выше температуры Тв, то в нем происходят пластические деформации, а напряжения снижаются вместе со снижением предела текучести (фиг. 2, г, кривая BD). Объем элемента все увеличивается благодаря увеличению поперечного сечения. После охлаждения такого элемента, длина его равна

где /0— длина элемента после охлаждения; TD — максимальная температура нагрева. Поперечное сечение становится больше первоначального (d'Q >d0), т. е. элемент получает остаточную деформацию1— увеличение диаметра и сокращение длины. После охлаждения до температуры ниже точки Е (фиг. 2, г) элемент потеряет контакт с опорными поверхностями и сокращается свободно при отсутствии внутренних напряжений. Если теперь подвергнуть нагреву по такому же температурному циклу элемент, жестко закрепленный в опорных поверхностях (т. е. элемент, не имеющий возможности ни удлиняться, ни  сокращаться по схеме на фиг. 3, а), то после прохождения