Системы управления электромеханическими объектами. Система управления «магнитный усилитель – двигатель», страница 15

и переходные процессы при пуске двигателя (б)

Переходные процессы при пуске двигателя в системе без обратных связей показаны  на рис. 9.2, б сплошными линиями. Здесь нарастание тока определяет постоянная времени цепи якоря T_я, а нарастание скорости вращения электромеханической постоянной времени T_м. При включении обратных связей (в частности, по скорости) быстродействие системы возрастает,  как показано пунктиром (см. рис. 9.2, б), т.е. время переходного процесса t_и2 меньше t_и1.

На рис. 9.3 приведена структурная схема трехконтурной системы автоматического управления (САУ) ДПТ, в которой можно выделить следующие узлы:

1 - структурная схема ДПТ как динамической системы с обратной связью по частоте вращения;

2 - коэффициенты передачи датчиков обратной связи;

3 - программная реализация регуляторов с помощью микроконтроллера (МК);

4 - силовой блок транзисторных ключей, осуществляющий ШИМ.

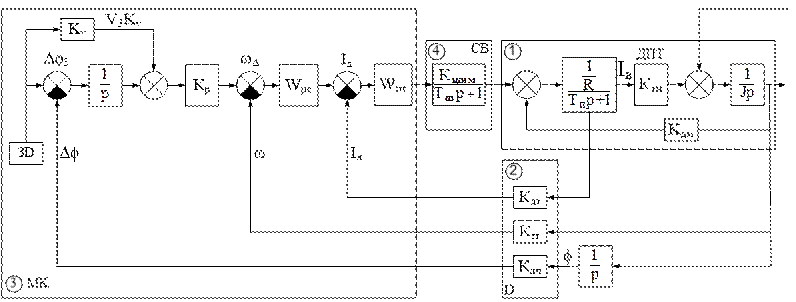
Рис. 9.3. Структурная схема следящего привода;

В общем случае в микроконтроллере реализованы три регулятора:

регулятор тока с передаточной функцией

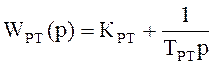;                                                          (9.3)

регулятор скорости

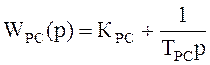;                                                           (9.4)

и регулятор следящий системы с коррекцией по скорости, который вырабатывает задание регулятору скорости w₃, согласно выражению

                                                            (9.5)

При необходимости простой стабилизации скорости вращения двигателя используется одноконтурная система с обратной связью по скорости, у которого

                                                                         (9.6)

Микроконтроллер также имеет в своем составе программный задатчик ‑ ЗД.

Оптимальный выбор коэффициентов передачи и постоянных времени регуляторов зависят от параметров объекта управления.

При синтезе ПИ-регуляторов тока и скорости используют принцип подчиненного управления, при котором каждый контур анализируется отдельно от остальных, начиная от внутреннего к внешнему.

Рассмотрим контур тока, показанный на рис. 9.4, а передаточная функция ДПТ по току будет иметь вид:

                                        (9.7)

Учитывая, что передаточная функция ПИ-регулятора тока описывается формулой (9.3), получим выражение для передаточной функции прямого канала контура тока (см. рис. 9.4, а)

                              (9.8)

Для повышения быстродействия системы выбирают параметры ПИ-регулятора так, чтобы компенсировать большую постоянную времени объекта управления – в данном случае T_м, так как обычно T_м >> T_я, т.е. принимают

                                                                          (9.9)

Тогда передаточная функция прямого канала контура тока примет вид

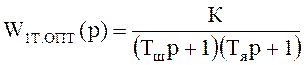, где

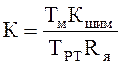
Передаточная функция замкнутого контура тока для этого случая будет

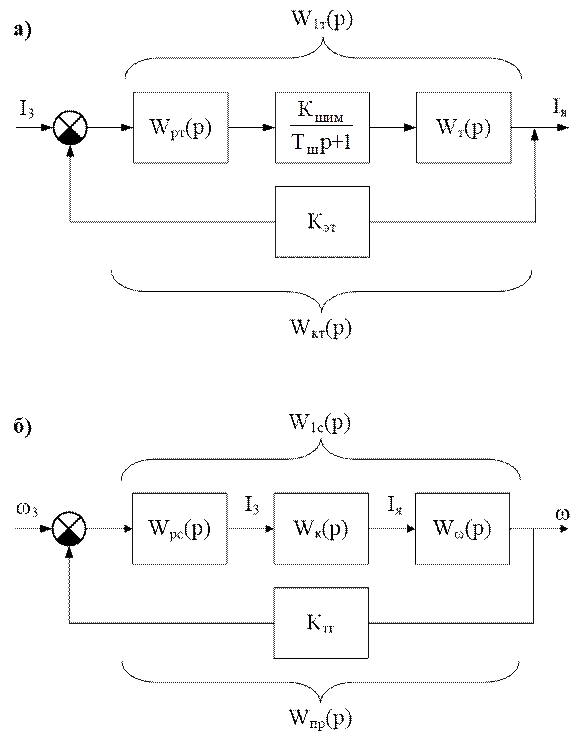
Рис. 9.4. Структурные схемы контуров тока (а) и скорости (б) системы управления ДПТ

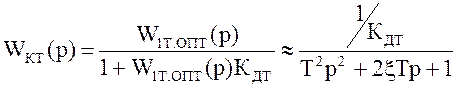, где

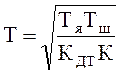, а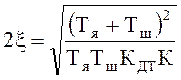

Оптимальным является соотношение, когда = 0,707, и

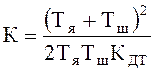                                                                                                            (9.10)

Тогда оптимальные параметры регулятора тока выбираются из соотношения (9.9) и (9.10), и полученная при этом передаточная функция контура тока будет

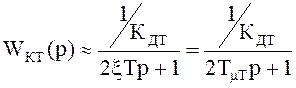,                                                                                                            (9.11)

так как при оптимальных параметрах

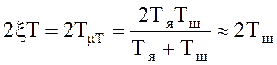
Рассмотрим контур скорости, показанный на рис. 9.4,б. Здесь W_pc(p) соответствует выражению (9.4), W_KT(p) – выражению (9.11), а W_w(p) – передаточная функция ДПТ от тока к скорости:

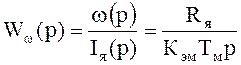                                                                                                            (9.12)

Произведя преобразования

, аналогичные анализу контура тока, получим оптимальные соотношения для параметров регулятора скорости