Математика \ Математическое моделирование

Построение двумерных графиков, их редактирование и измерения на графике, страница 17

Возможен вариант двукратного интегрирования без использования цикла for: см. рис. 4.5,Б. Однако, выходная таблица интегрирования – не вектор, и для формирования ИТВ данные этой таблицы следует передать во входную таблицу, согласно п. 3 разд. 4.1.2.

Имена расчетных таблиц 2, 3, 4-го этапов и ИТВ помещены над таблицами для сокращения площади, занимаемой таблицами, с помощью  команд контекстного меню заголовка строки или столбца таблицы (указатель мышки нужно поместить в эти места перед вызовом меню) Alignment-Above.

4.3.2. Тройной интеграл

Вычисление тройного интеграла [33, с. 632, формула (2.3.2.2)] с тремя параметрами методом квазивекторизации с оценкой погрешности пред­ставлено на рис. 4.6. Формула (4.7) – точное выражение этого интеграла, значения которого для векторов параметров вычислены посредством векторизации на этапе 2.

 


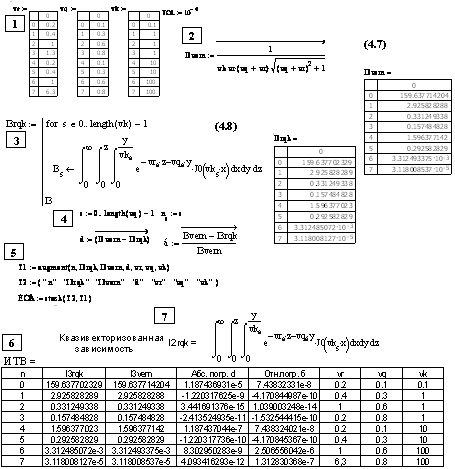Рис. 4.6. Этапы 3-параметрического 3-кратного квазивекторизованного интегрирования                            для тройного интеграла (4.8) с параметрами (vr, vq, и vk) и с построением таблицы ИТВ;                                       режим автовыбора, метод – адаптивный, TOL = 10-4 

Несмотря на то, что системная погрешность вычислений TOL = 10-4 , относительная погрешность вычисления интеграла в 10 и более раз меньше – см. столбец 4 ИТВ рис.4.6 (выражения для обеих погрешностей введены в РДМ на 4-м этапе).

 Таблица ИТВ вставлена  в Word-до­кумент через Excel, так как прямая вставка из Mathcad не помещается в формате листа, уменьшение же размеров до приемлемых сильно уменьшает размер букв текста.

4.3.3. Пятикратный интеграл

Вычисление двух вариантов 5­кратного интеграла представлено на рис. 4.7,А и Б: объемы 5-мерных параллелепипеда и шара единичного радиуса. В случае шара Mathcad не смог вычислит интеграл, и размерность шара пришлось уменьшить до 4. Порядок ввода объектов помечен номерами. Точные значения параллелепипеда и шара вычислялись по формулам (4.9) и (4.11), соответственно. Данные по точности и времени вычисления двух типов интегралов от двойного до 5-кратного представлены в табл. 4.2. Время измерялось посредством функции пакета time(…) (правила применения time(…) – см. далее).

Скачать файл