Шаблон для многократного интегрирования вызывается многократным нажатием клавиши <&>. Принципы однократного интегрирования (см. разд. 4.1) действительны и для многократного. В справке Mathcad 13 не указаны границы кратности интегрирования, но, как показывают примеры рис. 4.5, 4.6, возможно вычисление двойных и тройных интегралов с приличной относительной погрешностью «б» от 1,04×10–14 до 3×10–4 при TOL = 10-4. Пакет уверенно вычисляет 4-кратный интеграл от простой функции, 5-кратный интеграл вычисляется пакетом неуверенно даже для простых функций (см. разд. 4.3), в связи с чем, границей рабочего диапазона кратности интегрирования в Mathcad 12 и 13 следует считать 4-кратное интегрирование.
Пример 2-кратного квазивекторизованного интегрирования для пяти параметров по выражению (4.6) с формированием ИТВ показан на рис. 4.5,А. Этапы ввода пронумерованы.
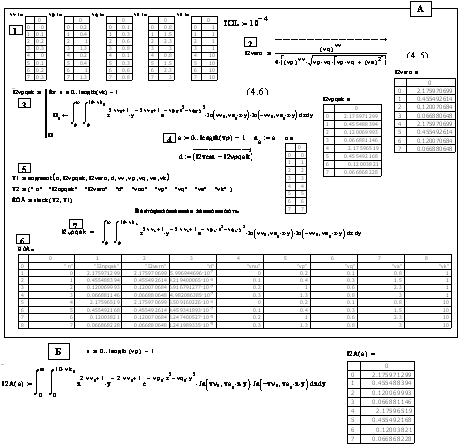 |
Рис. 4.5. А – этапы 5-параметрического 2-кратного квазивекторизованного интегрирования для двойного интеграла (4.6) с параметрами (vn, vp, vq, va и vk) и с построением таблицы ИТВ; режим автовыбора, метод – адаптивный; Б – вариант интегрирования с использованием рядной переменной s
Этап 2 не обязателен: выражение (4.5) является точным значением двойного интеграла из (4.6) [33, с. 623, ф. 8] при бесконечном значении верхнего предела внутреннего интеграла и служит для оценки точности интегрирования по (4.6) – см. столбец 3 в ИТВ. Погрешность d вычисляется на этапе 4 и лежит в диапазоне 4,5×10–7…3,3×10–5, причем, погрешность интегрирования и вычисления по формуле (4.5) TOL = 10-4.
Замена бесконечного верхнего предела во внутреннем интеграле на 10νkS в (4.6) вызвана отказом Mathcad интегрировать в связи с получением при интегрировании числа, большего пакетной бесконечности 10307.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.