Методические рекомендации к выполнению лабораторных работ по дисциплине "Сопротивление материалов". Часть 2

СОДЕРЖАНИЕ

Лабораторная работа № 14 Определение перемещений в пространственной статически определимой системе	4
ОПРЕДЕЛЕНИЕ ОПОРНЫХ РЕАКЦИЙ В СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ БАЛКАХ	6
Лабораторная работа № 15 Определение реакции промежуточной опоры двухпролетной неразрезной балки с консолями
Лабораторная работа № 16 Определение опорного момента балки с одним защемленным и другим опертым концами	9
Лабораторная работа № 17 Определение опорных реакций и перемещений в статически неопределимой балке при наличии зазора между балкой и опорой	12
Лабораторная работа №18. Косой изгиб консольной балки	17
Лабораторная работа № 19 Внецентренное растяжение стальной полосы	19
Лабораторная работа №20 Изгиб плоского кривого стержня	22
Лабораторная работа № 21 Определение величины критической силы для сжатого стержня с шарнирно закрепленными концами	26
Лабораторная работа №22 Ударная проба материала на излом	29
Лабораторная работа № 23 Исследование колебаний балки с одной степенью свободы	32
Лабораторная работа № 24. Исследование явления усталости металлов. Определение предела выносливости при симметричном цикле	40

Лабораторная работа № 14.

ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ В ПРОСТРАНСТВЕННОЙ СТАТИЧЕСКИ ОПРЕДЕЛИМОЙ РАМЕ

Цель работы: экспериментальное определение вертикального, горизонтального и углового перемещения заданного сечения в пространственной статически определимой раме.

Описание конструкции и приборов.

Пространственная рама состоит из трех стержней одинакового диаметра d, жестко соединенных между собой в узлах (рис.14.1). Левый конец конструкции жестко защемлен. Консольная часть в сечении А, нагружается силой F.

Рис. 14.1                                           Рис. 14.2

Углы поворота с достаточной точностью могут быть найдены с помощью рычага (рис.14.2) и двух индикаторов или прогибомеров. Такой угломер предложил Аистов. В работе использован рычаг длиной . Деформации измеряются стрелочными индикаторами часового типа с ценой деления 0,01 мм. Тогда точность измерения угла поворота составит  рад, или семь секунд. Перемещение сечения А измеряется прогибомером Максимова с ценой деления 0,1 мм. Такие прогибомеры могут закрепляться на конструкции или неподвижном основании, в зависимости от условий эксперимента.

Порядок проведения эксперимента

С помощью линейки студенты уточняют длину каждого участка (расстояние между серединами угловых точек) и наносят их на расчетную схему (рис. 14.1). Длины всех участков выражаются через пролет l .

В таблицу записываются показания всех приборов до и после приложения силы F.

Если снять нагрузку с конструкции и равноплечего рычага, то показания приборов возвращаются к первоначальным (исходным) отсчетам. Это подтверждает упругую работу конструкции.

Обработка результатов опыта

Разности отсчетов, полученных при нулевой и заданной нагрузке F соответствуют перемещениям сечений в статически определимой системе. Угол поворота вычисляется по формуле .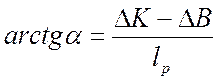

Теоретические расчеты

В заданной системе строятся эпюры изгибающих и крутящего моментов от внешней нагрузки (рис.14.3,б) и единичных воздействий, приложенных по направлению искомых перемещений (рис.14.3, в, г, д, е).

Эпюры изгибающих моментов строят в плоскости изгиба со стороны растянутого волокна. Положительным принят крутящий момент, вызывающий поворот стержня вокруг его оси против часовой стрелки. Тогда, перемещение в сечении А от  записывается:

.

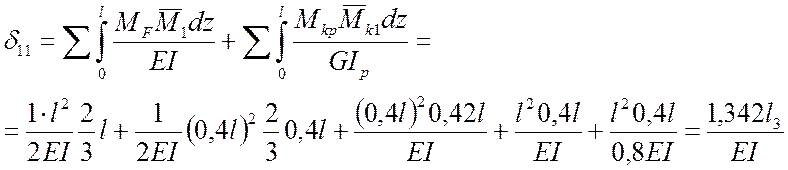Теоретические значения  и  студентам предлагается найти самостоятельно.

В качестве вывода теоретические значения перемещений сравниваются с экспериментальными и определяется величина погрешности, возникающей из – за того, что при вычислении перемещений не учитывается влияние продольной и поперечной сил на деформацию конструкции.

Рис. 14.3

Контрольные вопросы

1.  Какие системы относятся к плоским и пространственным?

2.  Для чего строят эпюры при вычислении перемещений в системе?

3.  Какие эпюры необходимо «перемножить» , чтобы получить перемещение?

4.  Какие можно использовать формулы для вычисления перемещения в балках и рамах?

5.  Как выбирается направление единичной силы?

6.  Сколько составляющих включает интеграл Мора для плоской системы?

7.  Чем отличается запись интеграла Мора для пространственной системы?

ОПРЕДЕЛЕНИЕ ОПОРНЫХ РЕАКЦИЙ В СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ БАЛКАХ

Исходные положения

При расчете статически неопределимых балок выполняется вполне определенная последовательность действий и рассуждений. Рассмотрим балку, защемленную одним концом и опирающуюся на промежуточную опору (рис. I, а).

Рис. I

Раскрытие статической неопределимости проводится в следующем порядке:

1.  Определяется степень статической неопределимости балки (в данном примере п=1).

2.  Путем отбрасывания тех или иных связей заданная статически неопределимая система превращается в статически определимую,  геометрически неизменяемую. Полученная система называется основной. Усилия в отброшенных связях называются "лишними" (с точки зрения статической определимости) неизвестными, и их наряду с другими внешними силами прикладывают к основной системе (в примере рис. I, б).

3.  Далее составляются условия совместности деформаций, отрицающие суммарные перемещения по направлению отброшенных связей от действия лишних неизвестных и заданных внешних сил. Для рассматриваемого примера , рис.I, б, в, г. После представления  в виде , где  - перемещение в статически определимой основной системе по направлению "лишней" неизвестной, вызванное единичным значением этой неизвестной, записывается уравнение совместности деформаций в канонической форме: . Отсюда 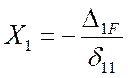. Перемещения  и  определяются по формуле Мора с использованием приема Верещагина.

Экспериментальное определение реакции «лишней» связи проводится в той же последовательности, что и теоретический расчет.

1.  Система имеет одну «лишнюю» связь (рис.II, а).

2.  Отбросим «лишнюю» связь, приняв за неизвестную реакцию в опоре  В. Получим основную систему (рис.II, б).

Под действием силы F, по направлению отброшенной связи, происходит перемещение  (рис.II, в), которое можно измерить, например, индикатором (рис.II, г). С помощью коромысла, закрепленного в точке В, устанавливая на поддон гири, подберем груз таким образом, чтобы сечение В балки вернулось в свое первоначальное положение, которое оно занимало до деформации. Нагрузка на поддоне соответствует величине искомой "лишней" неизвестной.

Рис. II

Лабораторная работа № 15.

ОПРЕДЕЛЕНИЕ РЕАКЦИИ ПРОМЕЖУТОЧНОЙ ОПОРЫ ДВУХПРОЛЕТНОЙ НЕРАЗРЕЗНОЙ БАЛКИ С КОНСОЛЯМИ

Лабораторная работа № №16.

ОПРЕДЕЛЕНИЕ ОПОРНОГО МОМЕНТА БАЛКИ С ОДНИМ ЗАЩЕМЛЕННЫМ И ДРУГИМ ОПЕРТЫМ КОНЦАМИ

Цель работ: оценить возможность применения метода сил для определения реакций в «лишних» связях в статически неопределимых системах.

Постановка и выполнение опытов

В лабораторной работе № 15 рассматривается балка, представленная на рис.15.1,а.