Методические рекомендации к выполнению лабораторных работ по дисциплине "Сопротивление материалов". Часть 2, страница 4

,                                          (18.1)

где , , , .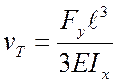

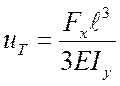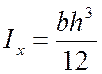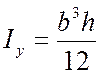Рис. 18.2

Угол наклона линии прогиба к вертикали вычисляется так:

,                                                (18.2)

где

;

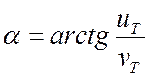- заданный угол.

В выводах следует отметить, насколько подтверждаются опытом теоретические результаты, полученные по формулам (18.1) – (18.2).

Контрольные вопросы.

1.  Какой изгиб называется косым?

2.  В чем принципиальное различие между плоским и косым изгибом?

3.  В чем заключается общий подход расчета стержней на сложное сопротивление?

4.  Каковы результаты опыта: как ориентирована плоскость изгиба оси балки при косом изгибе?

5.  Как теоретически определяется положение нейтральной линии при косом изгибе, а также величина и направление полного прогиба ?

Лабораторная работа № 19.

ВНЕЦЕНТРЕННОЕ РАСТЯЖЕНИЕ СТАЛЬНОЙ ПОЛОСЫ

Цель работы: экспериментальное определение нормальных напряжений в случае внецентренного растяжения стержня и сравнение опытных данных с теоретическими.

Постановка опыта

В опыте используется стальной образец прямоугольного поперечного сечения (рис.19.1).

Экспериментальное определение нормальных напряжений  сводится к измерению относительных продольных линейных деформаций на каждой ступени нагружения с последующим применением закона Гука в форме , где Е – модуль продольной упругости. Линейные деформации измеряются на боковых гранях, перпендикулярных плоскости изгиба, где влияние эксцентриситета наиболее сильно сказывается.

Рис. 19.1

Для измерения линейных деформаций используются рычажные тензометры А₁, А₂.

Порядок проведения опыта и обработка результатов.

. Записываются показания тензометров при начальной нагрузке.

Увеличивается нагрузка, записываются отсчеты по приборам, затем  образец разгружается до начальной нагрузки, здесь необходимо проследить, чтобы показания приборов вернулись к начальным отсчетам.

Подсчитывается величина абсолютного удлинения  и укорочения базовой длины стержня, как отношение разности показаний приборов  к коэффициенту увеличения К.

Определяется относительная деформация растянутой и сжатой граней, как отношение абсолютного удлинения (укорочения) к длине соответствующей базы прибора , .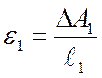

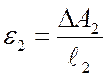С помощью закона Гука определяются величины наибольших нормальных напряжений в сжатой зоне  и в растянутой зоне .

Теоретическое определение нормальных напряжений

 Теоретическое определение наибольших напряжений при внецентренном растяжении (сжатии) определяется по формулам

 

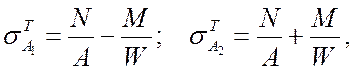
где

 - продольная сила;

 - изгибающий момент ;

 - площадь поперечного сечения;

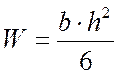- момент сопротивления прямоугольного сечения.

В выводах требуется отметить, надежными ли являются расчетные формулы для нормальных напряжений в случае внецентренного растяжения образца. Указать расхождение в процентах между опытными и теоретическими значениями напряжений.

Контрольные вопросы.

1.  Какова цель опыта?

2.  Какой вид деформации называется внецентренным растяжением?

3.  Какие внутренние усилия возникают в стержне при внецентренном растяжении (сжатии)?

4.  . Какие измерительные приборы использовались в опыте?

Лабораторная работа №20.

ИЗГИБ ПЛОСКОГО КРИВОГО СТЕРЖНЯ

Цель работы: экспериментальное определение нормальных напряжений и перемещений в кривых стержнях большой кривизны..

Постановка опыта

Испытанию подвергается стальной кривой брус в виде разрезанного кольца, имеющего прямоугольное поперечное сечение с  (рис. 20.1). При таком отношении высоты сечения  к среднему радиусу  влияние кривизны сказывается достаточно заметно. Нагрузка к кольцу прикладывается в вертикальной диаметральной плоскости, как показано на рис.20.1, с помощью винтовой машины. Характер распределения нормального напряжения выявляется посредством измерения деформаций в точках  опасного сечения "a - a" бруса с последующим применением закона Гука.

Рис. 20.1

Наиболее подходящим в данном случае является электротензометрический метод измерения деформаций, основанный на преобразовании механических перемещений в изменение омического сопротивления. Этот метод подробно описан в лабораторной работе № 9.

Порядок проведения опыта и обработка результатов.

Производится обмер кривого бруса и расстояний между рабочими датчиками. Результаты заносятся в журнал наблюдений.

К брусу прикладывается  начальная нагрузка, в журнал испытаний заносятся начальные показания в шести точках, где наклеены тензодатчики, и показания  индикатора часового типа (рис. 20.1).

Нагрузка увеличивается, после чего снимаются и записываются в журнал наблюдений показания каждого рабочего датчика и индикатора.

Подсчитываются приращения (по отношению к начальной нагрузке F=10 кН) показаний приборов.

Определяются опытные значения нормальных напряжений  в точках  опасного сечения кольца и вертикальное перемещение w концевых сечений кольца.

Полученные экспериментальные результаты записываются в журнал наблюдений.

Теоретическое определение напряжений и
вертикального перемещения концов бруса.

Теоретические величины нормальных напряжений сечения "a - a" (рис.20.1) в шести точках вычисляются по формуле:

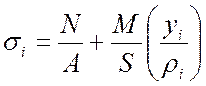,                                 (20.1)

где

 - продольная сила в опасном сечении "a - a";

 - изгибающий момент в сечении "a - a";

- площадь сечения;

 - статический момент сечения "a - a" относительно его нейтральной линии;

- радиус нейтральной линии кривого бруса;

 -  радиусы наружного и внутреннего контуров кольца;

- текущий радиус (рис.20.1);

 - расстояние от нейтральной линии сечения "a - a" до точек, в которых вычисляются значения напряжений.

Полученные теоретические значения нормальных напряжений записываются в журнал наблюдений. Величина взаимного вертикального перемещения w_А концов кривого бруса вычисляется по формуле Мора .

 В кривом брусе  перемещения, обусловленные сдвигом и растяжением, малы по сравнению с изгибными. Это приводит к возможности использовать только один из шести интегралов Мора (энергия кручения и изгиба в другой плоскости равна нулю).

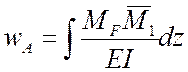.                                         (20.2)

Кроме того, учитывая симметрию формы и нагружения кольца расчетную схему можно упростить (рис.20.2, б).