УДАРНАЯ ПРОБА МАТЕРИАЛА НА ИЗЛОМ
Цель работы: определение ударной вязкости материала.
При динамическом приложении нагрузки, поведение материала, его механические характеристики могут существенно отличаться от полученных при статическом испытании. Так, при увеличении скорости растяжения возрастают характеристики прочности, убывают характеристики пластичности, то есть материал при динамическом приложении нагрузки становится более хрупким, чем при статическом воздействии. На такое поведение материала при динамическом нагружении влияет ряд факторов: - наличие концентраторов напряжений (надрезов, пазов, отверстий и т.п.), скорость приложения нагрузки, наличие остаточных напряжений, возникающих при закалке, при наклепе, а также химический состав стали (например, наличие примесей фосфора).
Одним из наиболее распространенных
испытаний, позволяющих оценить сопротивление материала динамическим нагрузкам,
является испытание на удар до разрушения. Иногда это разрыв ударом, но чаще
излом ударом. Кратковременность испытания не позволяет определить деформации и
напряжения в момент удара, поэтому для оценки сопротивления материала излому
ударом вводится новая механическая характеристика - ударная вязкость. Величина ударной вязкости 
измеряется
отношением количества энергии Т, затраченной на излом образца, к площади
поперечного сечения образца A в месте излома
.
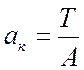Постановка испытания
Образец, предназначенный для испытания на излом ударом, имеет форму бруска прямоугольного поперечного сечения. В средней части образца, в сечении, по которому производится удар, делается прорезь той или иной формы. Назначение ее, создать в месте удара трехосное напряженное состояние, вызвать резкую концентрацию напряжений и локализовать пластические деформации в малом объеме. Именно эти факторы создают наиболее тяжелые условия для работы материала при динамических нагрузках, способствуют хрупкому разрушению при ударе.
Наиболее распространенный вид образца с надрезом для испытания на излом ударом и схема его установки на маятниковом копре представлены на рис.22.2.
|
|
|
Рис. 22.1 Рис. 22.2 |
Для проведения испытания используется
маятниковый копер. Принцип действия маятникового копра следующий. Маятник весом
G (рис.22.1) поднимается в исходное положение на
некоторую высоту 
. При свободном падении
маятник в самой нижней точке траектории своего движения разрушает образец и,
продолжая движение, понимается на высоту 
.
Работа, затраченная на излом образца, измеряется разностью величин энергий,
которыми обладает маятник до и после удара:
,
где Тс – энергия, затрачиваемая на преодоление вредного сопротивления (сил трения).
Для измерения работы, затраченной на
излом образца, служит специальное приспособление, которым снабжен маятниковый
копер. Указатель приспособления показывает на шкале в определенном масштабе
разность высот падения и подъема маятника 
(см.
рис.22.1), а следовательно, и величину работы Т, затраченной на излом
образца. Градуировка шкалы выполнена так, что она позволяет читать величину работы,
затраченной на излом образца, причем потери энергии Т0 на
сопротивление трению учтены при градуировке шкалы, как постоянная поправка.
Методика проведения опыта
Для опыта подготавливают обычно два образца из сталей, отличающихся своей способностью противостоять ударным нагрузкам. Измеряют размеры образцов в ослабленном сечении.
Один из образцов устанавливают на опорах маятникового копра так, чтобы удар приходился точно по ослабленному сечению со стороны, противоположной вырезу (см. рис.22.2).. Маятник копра поднимают и закрепляют специальной защелкой с фиксатором. Перед пуском маятника освобождают предохранительный фиксатор и специальным спусковым устройством освобождают защелку. Маятник падает и разбивает образец. По измерительному устройству определяется работа, затраченная на излом. Аналогично испытывается и второй образец. Работа, затраченная на излом образцов, делится на площадь ослабленного сечения и, таким образом, определяется величина ударной вязкости материала.
Интересно познакомиться с графиком
зависимости величины ударной вязкости от
температуры испытания t˚
(рис.22.3).
|
|
|
Рис. 22.3 |
Из этого графика видно, что в сравнительно узком интервале температуры, расположенном в области отрицательных температур, наблюдается резкое снижение ударной вязкости материалов. С этим явлением связана так называемая хладноломкость рельсов, бандажей и других деталей конструкций железнодорожного пути и подвижного состава, неоднократно наблюдавшаяся на транспорте в зимних условиях и приносившая много неприятностей.
Сравнение результатов опыта и выводы
В заключение необходимо выяснить, какой из испытанных образцов показал более высокую ударную вязкость; оценить применимость испытанных материалов для строительных целей. При этом необходимо учитывать, что металл строительных конструкций должен иметь значение ударной вязкости не менее 100Дж/см2.
1. Что называется ударной вязкостью материала?
2. В чем состоит особенность поведения материала при ударных нагрузках?
3. Опишите стандартную форму образца для испытания на ударную пробу. Для какой цели на образце делается надрез?
4. Как определяется работа, затраченная на излом образца?
5. Как зависит ударная вязкость материала от температуры, при которой она определяется?
ИССЛЕДОВАНИЕ КОЛЕБАНИЙ БАЛКИ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ
Цель работы: демонстрация явления резонанса, экспериментальное определение частот свободных и вынужденных колебаний, логарифмического декремента колебаний, оценка динамических напряжений при резонансе.
Вспомним некоторые основные положения и закономерности теории колебаний упругих систем с одной степенью свободы, которые потребуются при выполнении и обработке опытов.
Упругая система может иметь одну, несколько или множество степеней свободы. Число степеней свободы - число независимых параметров, определяющих положение в пространстве упругой системы в любой момент колебательного процесса. Реальные упругие системы имеют бесчисленное множество степеней свободы, но если принять массу колеблющейся системы не распределенной, а сосредоточенной в одной или нескольких точках, что допустимо при определенных условиях, то появляется возможность говорить об ограниченном числе степеней свободы упругой системы.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
