Методические рекомендации к выполнению лабораторных работ по дисциплине "Сопротивление материалов". Часть 2, страница 7

Различают колебания свободные и вынужденные. Свободные колебания возникают в результате однократного импульсного силового воздействия на упругую систему, выводящего ее из состояния равновесия. Вынужденные колебания возникают в упругой системе под действием меняющейся по периодическому закону возбуждающей силы.

Рис.23.1

Свободные колебания упругой системы с одной степенью свободы (например, изображенной на рис.23.1) с учетом сил сопротивления среды описываются следующими зависимостями:

,                                             (23.1)

где

 - смещение массы т в любой момент времени , отсчитываемого от начала свободных колебаний;

          - основание натурального логарифма;

         - коэффициент, характеризующий сопротивление среды;

    - амплитуда колебаний без учета сил сопротивления, при ;

    - круговая частота свободных колебаний в сопротивляющейся среде, связанная с  соотношением

,                                        (23.2)

Здесь  – круговая частота свободных колебаний в несопротивляющейся среде (при ),

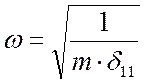,       или 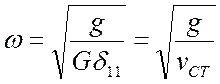        ,          (23.3)

где

 - ускорение свободного падения;

 - перемещение точки С в рассматриваемой системе от статического действия силы, равной единице (рис.23.2, а);

 - прогиб в точке С рассматриваемой системы от статического действия нагрузки G (рис.23.2, б).

Частота свободных колебаний системы с одной степенью свободы с учетом сил сопротивления определяется зависимостью

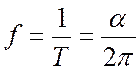,                                              (23.4)

а без учета сил сопротивления среды, из (23.4) и (23.2), при , получаем

,

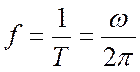или, с учетом (23.3),

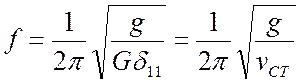.                                   (23.5)

Под силами сопротивления среды понимают  силы внутреннего трения материала упругой системы, силы трения в опорах, в узлах колеблющейся системы, силы сопротивления внешней среды.

Рис. 23.2

Как следует из (23.1), свободные колебания при  затухают во времени (рис.23.3).

 Скорость затухания колебаний характеризуется отношением амплитуд колебаний  и , отстоящих друг от друга на интервал времени Т, равный периоду колебаний:

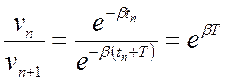,                                                     (23.6)

отсюда

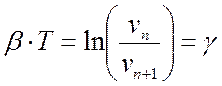                                                        (23.7)

Рис. 23.3

Величину  называют логарифмическим декрементом колебаний. Найти ее можно только экспериментально.

Вынужденные колебания упругой системы с одной степенью свободы создаются силой  F,  меняющейся по закону синуса (рис.23.4).

Здесь:

 - циклическая частота возбуждающей силы;

 - статический прогиб в месте приложения нагрузки, от наибольшего значения возбуждающей силы.

Наибольшая амплитуда вынужденных колебаний А определяется  по формуле

,                                                 (23.8)

где  μ - коэффициент нарастания амплитуды вынужденных колебаний.

Если учесть статический прогиб балки от собственного веса , около которого происходят вынужденные колебания, то максимальный прогиб балки

.                                              (23.9)

где

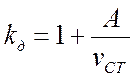 ,                                            (23.10)

или с учетом (23.8)

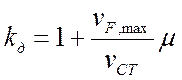.                                       (23.11)

Наибольшие напряжения при вынужденных колебаниях определяются зависимостью

.                                               (23.12)

Рис. 23.4

Постановка опыта.

Опыт проводится на установке, схема которой изображена на рис. 23.5.

Гибкая стальная балка АВ пролетом lшарнирно закреплена по концам, имеет поперечные размеры: ширину b и высоту h . Вес балки . В середине балки подвешен мотор с грузами  (общий вес )  и эксцентрики  (их вес ). Эксцентрики отстоят от оси вращения на расстояние r .

При включении электромотора  эксцентрики  начинают вращаться с угловой скоростью n . Центробежная сила инерции, возникающая  в них,

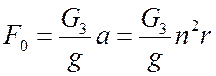                                        (23.13)

дает вертикальную составляющую, перпендикулярную к продольной оси балки АВ, меняющуюся по гармоническому закону

,                                                 (23.14)

Рис. 23.5

Под действием этой возбуждающей силы F возникают вынужденные колебания с частотой

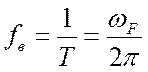,                                                        (23.15)

С помощью реостата можно менять угловую скорость вращения эксцентриков, а, следовательно, и частоту вынужденных колебаний балки .

Для записи диаграмм колебаний имеется вращающийся с постоянной окружной скоростью барабан . Барабан приводится в движение электромотором. Пишущий узел вычерчивает диаграмму колебаний.

Методика проведения опытов и их результаты

Сначала исследуем свободные колебания балки АВ. Не включая электромотор, отклоним балку АВ от положения равновесия и отпустим ее. Приведем в движение барабан и запишем диаграмму свободных колебаний системы (рис.23.6,а). Учитывая величину окружной скорости вращения барабана, найдем из полученной при эксперименте диаграммы среднее число колебаний в единицу времени. Эта величина и будет частотой свободных колебаний исследуемой системы. Из обработки той же диаграммы найдем и логарифмический декремент колебаний γ. При этом, для повышения точности определения величины γ измерение амплитуд свободных колебаний произведено на расстоянии не  одного, а  периодов. Тогда

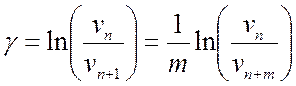.                                (23.16)

Проведем другой опыт, в котором будем наблюдать вынужденные колебания. Включим мотор и с помощью реостата зададим малое число оборотов эксцентрикам. Балка АВ будет совершать вынужденные колебания с малой амплитудой и частотой колебаний .Постепенно наращивая число оборотов эксцентриков, доведем его до такой величины, при которой амплитуда колебаний балки АВ достигает максимума, что будет соответствовать состоянию резонанса. Затем значительно увеличим число оборотов эксцентриков. При этом амплитуда вынужденных колебаний резко уменьшится. На каждом из этапов этого испытания записывается диаграмма вынужденных колебаний, примерный вид которой показан на рис.23.6, б.

 Из обработки этой диаграммы найдем частоты f_i(число колебаний в 1 с) и амплитуды колебаний  на каждом из наблюдавшихся этапов вынужденных колебаний (на рис.23.6 ). При тщательном выполнении опыта можно заметить, что частота вынужденных колебаний при резонансе окажется равной частоте свободных колебаний системы (на рис. ). Значения  и  заносятся в журнал наблюдений.