|
а) |
|
|
б) |
|
|
в) |
|
|
Рис. 20.2 |
|
Область интегрирования АС в
этом случае следует разбить на два участка АВ и ВС. Однако, поскольку
изгибающий момент ![]() на участке АВ равен нулю,
интегрирование остается провести только на участке ВС. За независимую
переменную удобно принять угол
на участке АВ равен нулю,
интегрирование остается провести только на участке ВС. За независимую
переменную удобно принять угол ![]() . При этом
. При этом ![]() . Выражения для изгибающего момента
. Выражения для изгибающего момента ![]() в сечении К от внешней силы
и от единичной силы
в сечении К от внешней силы
и от единичной силы ![]() получат вид
получат вид
![]() ;
; ![]() .
.
Подставляя ![]() ,
, ![]() ,
, ![]() в
(20.2), получим
в
(20.2), получим
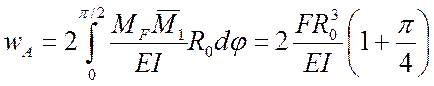 (20.3)
(20.3)
Полученное теоретическое значение перемещения ![]() надо записать в журнал наблюдений.
надо записать в журнал наблюдений.
Сравнение результатов и выводы.
Экспериментальные значения
нормальных напряжений ![]() в шести точках сечения "a - a" и перемещение
в шести точках сечения "a - a" и перемещение ![]() следует сравнить с теоретическими,
определить величину расхождения в процентах и прокомментировать результаты.
следует сравнить с теоретическими,
определить величину расхождения в процентах и прокомментировать результаты.
В выводах надо отметить, какова надежность расчетных формул сопротивления материалов для определения нормальных напряжений в кривых стержнях большой кривизны.
1. Скажите, посредством чего выявляется особенность распределения нормального напряжения в опасном сечении бруса?
2. Какой метод использован для измерения деформаций, на чем он основан?
3. Как в данном опыте была найдена теоретическая величина радиуса кривизны нейтрального слоя? Как получена эта формула?
4. Как теоретически определяется перемещение в кривом стержне ?
ОПРЕДЕЛЕНИЕ ВЕЛИЧИНЫ КРИТИЧЕСКОЙ СИЛЫ СЖАТОГО СТЕРЖНЯ С ШАРНИРНО ЗАКРЕПЛЕННЫМИ КОНЦАМИ
Цель работы: экспериментальное изучение процесса потери устойчивости при осевом сжатии стержня большой гибкости и определение величины критической силы.
Известно, что при продольном осевом сжатии достаточно длинных стержней исчерпание их несущей способности происходит из–за внезапного искривления оси (изгиба) первоначально прямого стержня.
Возникающие при этом напряжения существенно меньше предела текучести или временного сопротивления материала стержня. Такое явление называют потерей устойчивости стержня, а силу, при которой оно происходит, - критической.
Существует три формы равновесия системы: устойчивая, безразличная, неустойчивая. Когда прямой стержень сжимается силой меньшей, чем критическая, он находится в устойчивом равновесии, т.е. будучи выведен внешним воздействием из состояния равновесия, он стремится вернуться в исходное положение. Если стержень сжимается силой большей, чем критическая, то при идеальных обстоятельствах его ось может сохранять прямолинейную форму равновесия, но это будет неустойчивое равновесие. При малейшем отклонении оси этого стержня от прямолинейного положения прогибы резко возрастут, стержень перейдет в устойчивое равновесие, но с изогнутой осью. В том же случае, когда на стержень действует сжимающая сила, равная критической, он будет находиться в безразличном состоянии равновесия, т.е. с равным успехом будет сохранять под действием этой силы как прямолинейную, так и слегка изогнутую форму оси.
Величина критической силы зависит от гибкости стержня ![]() , от модуля упругости
, от модуля упругости ![]() , предела пропорциональности
, предела пропорциональности ![]() и предела текучести
и предела текучести ![]() материала. Гибкость стержня зависит
от способа закрепления стержня, его длины, формы и размеров поперечного
сечения:
материала. Гибкость стержня зависит
от способа закрепления стержня, его длины, формы и размеров поперечного
сечения:
 ,
,
где
![]() - коэффициент
приведения длины;
- коэффициент
приведения длины;
![]() - длина стержня;
- длина стержня;
![]() - минимальный
радиус инерции поперечного сечения стержня.
- минимальный
радиус инерции поперечного сечения стержня.
Для стержней большой гибкости (для стали ![]() ) величина критической силы
определяется по формуле Эйлера
) величина критической силы
определяется по формуле Эйлера
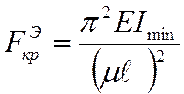 .
.
При
этом критическое напряжение удовлетворяет неравенству ![]() и
определяется зависимостью:
и
определяется зависимостью:
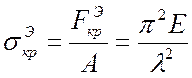 .
.
|
|
|
Рис. 21.1 |
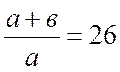 .
.Для исследования процесса потери устойчивости и определения величины критической силы исследуемый стержень нагружается постепенно возрастающей нагрузкой. На каждой ступени нагружения надо слегка изогнуть стержень. Если стержень возвращается в исходное, прямолинейное положение, это означает, что сила еще не достигла критического значения.
Действуя таким образом, надо подобрать величину сжимающей силы, при которой стержень, будучи слегка отклонен от прямолинейного состояния, сохранит это искривленное положение.
Найденное из опыта критическое значение сжимающей
силы ![]() записывается в журнал (
записывается в журнал (![]() - вес гирь на поддоне; 26 – передаточное
число нагружающего рычага).
- вес гирь на поддоне; 26 – передаточное
число нагружающего рычага).
Подсчитывается опытное значение критического напряжения
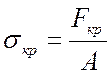 .
.
Чтобы правильно выбрать расчетную формулу для
определения критического напряжения, необходимо найти гибкость исследуемого
стержня  .
.
При шарнирном закреплении концов стержня коэффициент
приведенной длины ![]() .
.
Минимальный радиус инерции поперечного сечения стержня
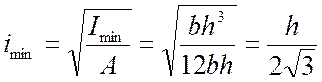 .
.
Подсчет показывает, что гибкость исследуемого
стального стержня более ![]() для стали.
Следовательно, для вычисления критического напряжения применим формулу Эйлера
для стали.
Следовательно, для вычисления критического напряжения применим формулу Эйлера
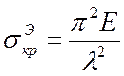 .
.
Критическую силу подсчитываем по формуле
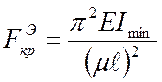 ,
,
Формула Эйлера для определения критической силы является
приближенной, так как при ее выводе использовалось приближенное дифференциальное
уравнение изогнутой оси стержня. Сопоставляя опытное значение критической силы ![]() с теоретическим
с теоретическим ![]() , найденным по формуле Эйлера, можно
дать оценку степени согласованности этих значений.
, найденным по формуле Эйлера, можно
дать оценку степени согласованности этих значений.
1. Назовите возможные формы потери устойчивости. В чем состоит суть явления потери устойчивости?
2. Что называется критической силой?
3. Как влияет способ закрепления стержня на величину критической силы?
4. При каком закреплении концов стержня критическая сила будет наименьшая?
5. Как влияет форма поперечного сечения сжатого стержня на величину критической силы при прочих равных условиях? По какому параметру можно произвести эту оценку?
6.
От каких параметров зависит
величина гибкости стержня ![]() ?
?
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.