Классификация систем автоматического управления. Условно-графическое представление САУ. Правила преобразования структурных схем, страница 8

И , наконец,  по  функциональной  схеме   можно   составить  структурную схему, представленную на рис.1.1.3.

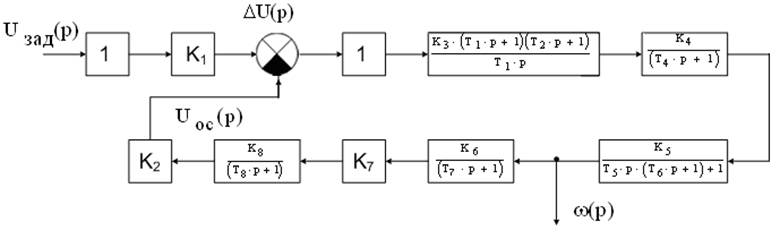
Рис.1.1.3. Линеаризированная структурная схема по функциональной схеме на рис.1.1.2.

На схеме обозначено:

1;1 – коэффициенты передачи ЗИ и АLА ,

К₁;К₂ – коэффициенты передачи УС,

К₃; Т₁; Т₂   –   коэффициент  передачи   и   постоянные   времени   ПИД (пропорционально-интегрально-дифференциального)-регулятора,

К₄; Т₄  – коэффициент  передачи   и   постоянная   времени тиристорного преобразователя, 

К₅;Т₅;Т₆ – коэффициент передачи и постоянные времени электродвигателя,

К₆;  Т₇   –  коэффициент  передачи  и  постоянная   времени  тахогенератора,

К₇ – коэффициент передачи датчика скорости.

К₈; Т₈  – коэффициент  передачи   и   постоянная   времени фильтра.

1.2.Основы операторно-частотного метода анализа и синтеза САУ.

Анализ и синтез САУ производят по математическим  моделям  с  помощью различных методов, приемов, критериев и правил.

Наиболее распространенными способами  математического  описания  САУ

для    анализа   и   синтеза   ее  являются     дифференциальные   уравнения, матричные  уравнения  и  структурные  схемы,  являющиеся  по  существу графической  интерпретацией  дифференциальных  уравнений  в операторной форме ( чаще всего по Лапласу).

Далее  нами  будет   использоваться   матмодель   САУ  в  виде  структурной схемы, для  построения  которой  необходимо  знать  передаточные  функции  элементов, как было показано в  п.1.1.

Рассмотрим  ряд  примеров  получения  передаточных  функций   элементов САУ.

Пример 1.2.1.

Найти передаточную функцию регулятора, построенного на операционном усилителе по схеме на рис.1.2.1., где обозначено : Z₁(p) и Z₂(p) - операторные сопротивления входное и обратной связи.

Рис. 1.2.1.  Операторная схема регулятора на операционном

усилителе ( вариант 1 ).

По методу узловых потенциалов,  считая, что в идеальном операционном усилителе ( ОУ )  R_вх→∞ и R_вых→0, можно записать:

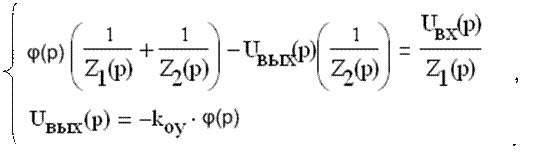
Для идеального ОУ коэффициент усиления k_оу→∞, тогда получим

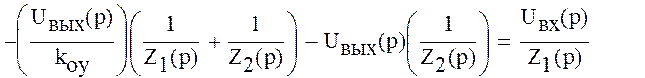
или

и окончательная передаточная функция будет

  .

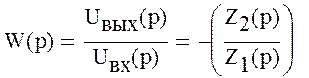Пример 1.2.2.

Найти передаточную функцию регулятора, построенного на операционном усилитиле  по схеме на рис. 1.2.2., где имеются дополнительные операторные сопротивления делителя  Z₃(p) и Z₄(p).

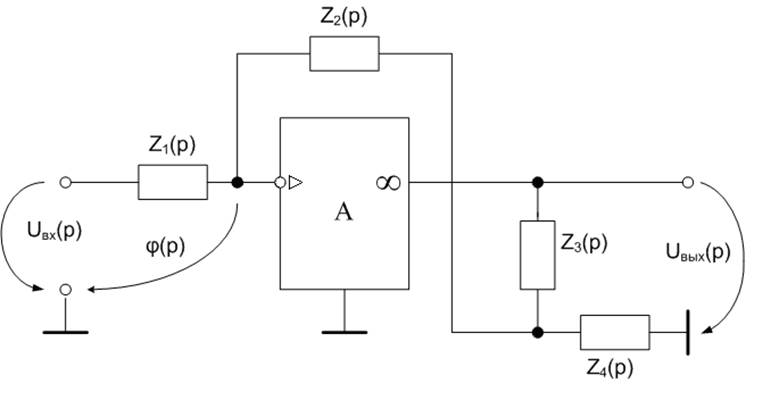
Рис.1.2.2.  Операторная схема регулятора на операционном

усилителе ( вариант 2 ).

Аналогично предыдущему запишем:

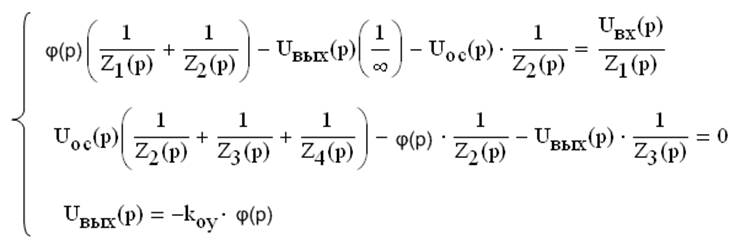
из первого уравнения при k_оу→∞ получаем

 ,

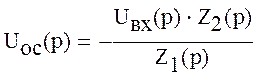тогда второе

.

Отсюда можно получить передаточную функцию 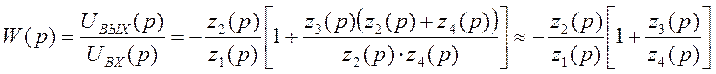,              так как обычно |z₂(p)|>>|z₃(p)+z₄(p)|.

Пример 1.2.3.

Найти передаточную функцию пропорционально-интегрального (ПИ) регулятора по схеме варианта 1(рис 1.2.1), для которого                                             .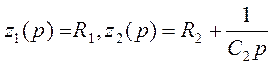

Согласно полученного в примере 1.2.1 .                                                             Обозначая

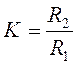 – коэффициент передачи регулятора,

 – постоянная времени регулятора, запишем передаточную функцию регулятора в виде

.

1.3. Преобразование структурных схем.

Начертание структурных схем можно упростить путем свертывания(“Упрощения”) их по правилам, приведенным в таблице 1.3.1.

Доказательства этих правил можно пояснить следующим.

Для последовательного соединения 3^х звеньев

.

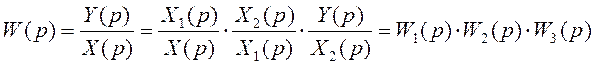Для параллельного соединения 3^х звеньев

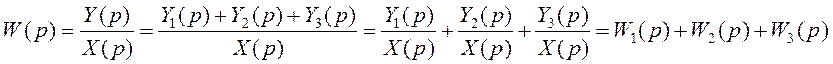
Правила в таблице 1.3.1. основные, так как они позволяют построить ряд частных, полезных, но редко используемых на практике правил.

Рассмотрим использование правил структурных преобразований на примере определения передаточной функции канала “момент – скорость” двигателя постоянного тока с независимым возбуждением по структурной схеме, полученной в дисциплине “Основы математического моделирования”.

Таблица 1.3.1.

 

Пример 1.3.1.

С помощью правил структурных преобразований найти передаточную функцию 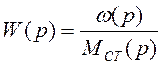 по структурной схеме канала ДПТ НВ.

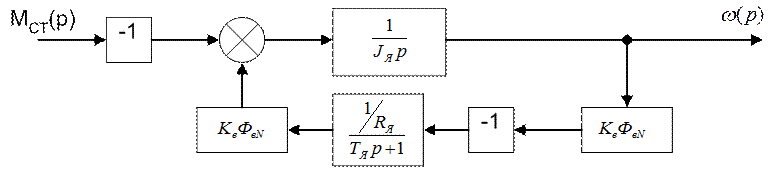
Рис 1.3.1. Структурная схема канала “момент – скорость” ДПТ НВ.