Классификация систем автоматического управления. Условно-графическое представление САУ. Правила преобразования структурных схем, страница 10

Ø  Амплитудно-фазо-частотная характеристика .

Ø  Статическая характеристика Х_ВЫХ(Х_ВХ) получается из передаточной функции W(p) заменой р→∞.

Ø  Переходная характеристика при Х_ВХ(t)=Х₀∙1(t) получается как , с помощью обратного преобразования по Лапласу.

Ø  По теореме о конечных значениях операторного преобразования по Лапласу Х_ВЫХ(+0)=Х₀∙W(p)|_p=∞, Х_ВЫХ(∞)=Х₀∙W(p)|_p=0

Ø  Весовая функция при Х_ВХ(t)=X₀∙δ(t) получается как .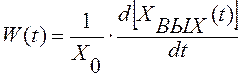

Отсюда следует, что W(p)=L{W(t)}, W(t)=L^-1{W(p)}, определяются через прямое и обратное преобразование по Лапласу.

1.5.2.Типовые линейные динамические звенья

Типовые динамические звенья подразделяются  согласно  виду  статических характеристик (X_вх-const) на

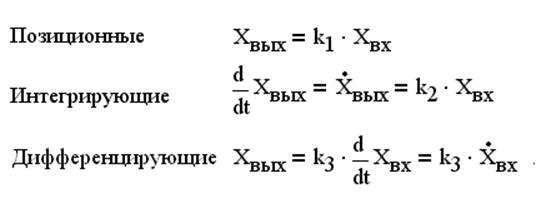
Эти характеристики имеют вид

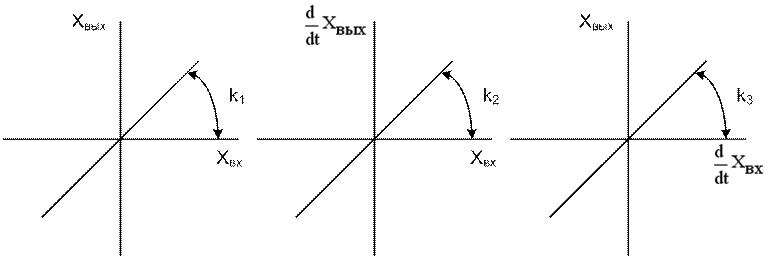
Рис.1.5.2.1. Статические характеристики типовых динамических звеньев

1.5.2.1. Позиционные динамические звенья

     а). Безинерционное звено

Это звено описывается  дифференциальным  уравнением  нулевого опрядка

К  таким  звеньям  относятся,    например,  рачаг,  потенциометр,  редуктор, электронный усилитель ( на малых частотах ), пропорциональный  регулятор   (П-регулятор).

В операторном виде уравнение звена запишется как

откуда передаточная функция

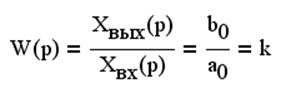
Где k – коэффициент передачи.

На рисунке 1.5.2.2. изображена схема П-регулятора, который имеет такую же передаточную функцию.

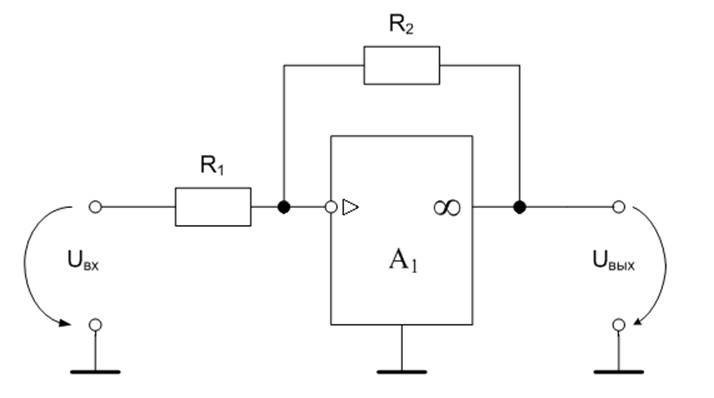
Рис1.5.2.2.  Принципиальная схема П-регулятора.

Действительно, в соответствии с ранее полученным здесь

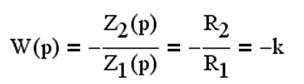
Знак минус возникает из-за реверсирования входного сигнала .

Характеристики безинерциального звена определим  через  W(p) с помощью выше изложенных взаимосвязей.

Статическая характеристика (X_вх-const)

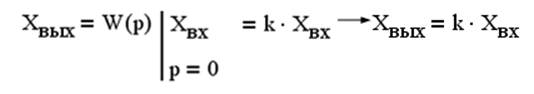
Амплитудно-фазочастотная характеристика

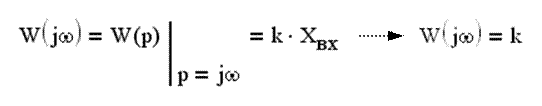
Амплитудно-частотная характеристика

Фазочастотная характеристика

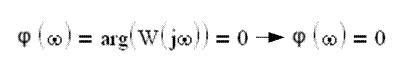
Логарифмическая амплитудно-частотная характеристика

 

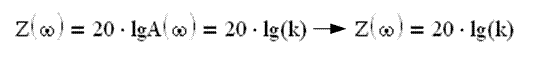
Логарифмическая фазочастотная характеристика

Переходная характеристика

Весовая характеристика

Эти характеристики обычно изображают графически

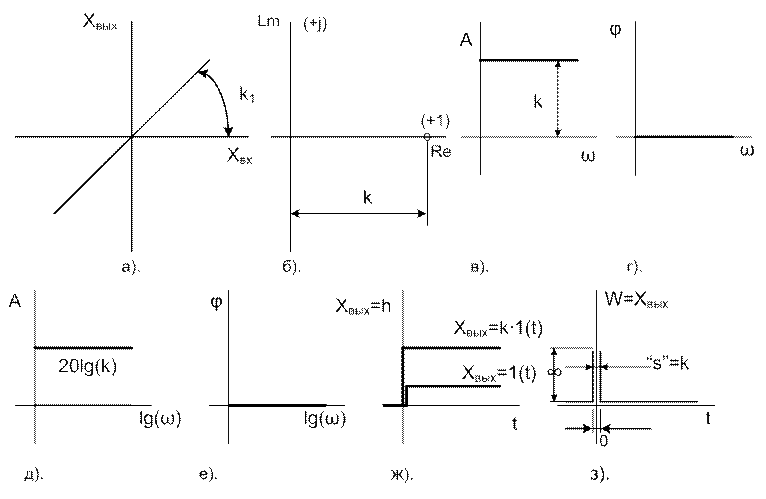
Рис.1.5.2.3. Характеристики безинерционного звена.

 По  характеристикам   видно,   что   реакция безинерционного   звена  на   входное    воздействие   любго  вида   сводится лишь к изменению  величины этого воздействия в “k” раз. Временные и частотные параметры  воздействия  остаются  без  изменения. 

     б). Апериодическое звено первого порядка

Это звено описывается дифференциальным уравнением первого порядка, имеющего вид

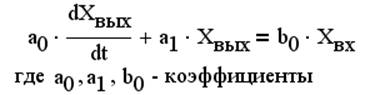
К таким звеньям относятся, например, якорная цепь ДПТ НВ, гидроусилитель, тахогенератор, тиристорный преобразователь, механизм с инерционной нагрузкой и жидкосным трением, апериодический фильтр (регулятор).

В операторном виде уравнение звена запишется как , откуда передаточная функция

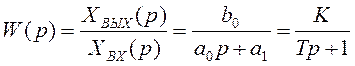, где

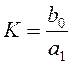 – коэффициент передачи,

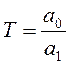 – постоянная времени.

На рисунке 1.5.2.4. изображена схема апериодического регулятора(фильтра), имеющего такую же передаточную функцию.

Рис. 1.5.2.4. Принципиальная схема апериодического регулятора.

Здесь по аналогии с предыдущим                                                                                 Где , .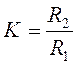

Характеристики апериодического звена первого порядка будут таковы:

Статическая характеристика

Амплитудно-фазочастотная характеристика

Амплитудно-частотная характеристика

Фазо-частотная характеристика

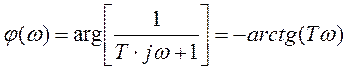
Логарифмическая амплитудно-частотная характеристика

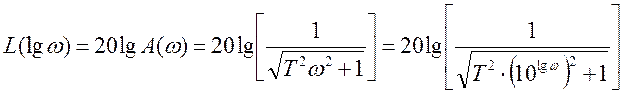
Логарифмическая фазо-частотная характеристика

Переходная характеристика

Весовая характеристика

Графический вид характеристик представлен на рис. 1.5.2.5.

Рис 1.5.2.5. Характеристики апериодичекого звена первого порядка.

По характеристикам видно, что реакция апериодичекого звена на входное воздействие замедленна(затянута). Величина этой реакции апериодичекого звена тем сильнее, чем больше частота входного сигнала. Действуя далее аналогичным образом, получим характеристики остальных типовых динамических звеньев, которые сведем в таблицы.