Конструктивные особенности и вычерчивание редуктора, страница 4

    [S_F ]'' – коэффициент, учитывающий способ получения заготовки зубчатого колеса, для поковок и штамповок [S_F ]'' = 1,0([2], табл. 3.4, с. 39)

Для шестерни

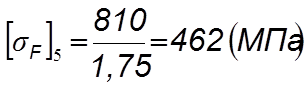
Для колеса

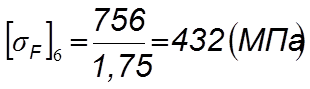
4.5.3.4 Находим отношения

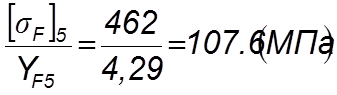                                        (4.51)

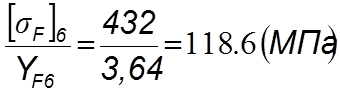                                        (4.52)

4.5.3.5 Дальнейшие расчеты ведем для зубьев шестерни, так как для него найденное отношение меньше.

4.5.3.6 Определяем коэффициент Y_b :

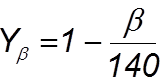                                                     (4.53)

где b - угол наклона делительной линии зуба, b = 8,019

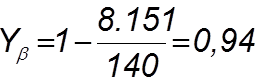
4.5.3.7 Определяем коэффициент К_Fa:

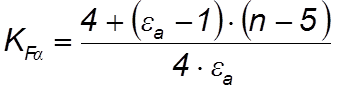                                        (4.54)

где e_а– коэффициент торцового перекрытия, e_а = 1,5;

    п – степень точности колес, п = 8

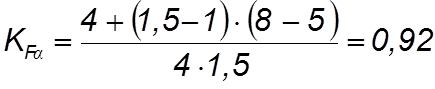
Проверяем зуб шестерни по формуле:

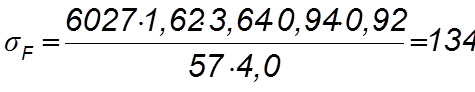
Расчет выполнен правильно, так как s_F < [s_F ] (134 < 701,5).

4.6 Выполняем проверочный расчет шестерни и колеса первой ступени

4.6.1 Проверяем контактные напряжения:

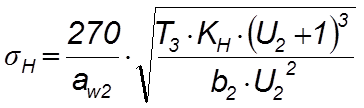                                    (4.55)

где К_Н – коэффициент нагрузки

                            К_Н = К_Нb× К_Нa× К_Нu                  (4.56)

где К_Нb - коэффициент, учитывающий распределение нагрузки по длине зуба, при y_bd = 1,2 и передаче с нессиметричным расположением колес по отношению к опорам К_Нb = 1,36 ([2], табл. 3.5, с. 39);

    К_Нa - коэффициент, учитывающий распределение нагрузки между зубьями, для косозубых передач с 8-ой степенью точности и окружной скоростью 0,2 м/с К_Нa = 1,06 ([2], табл. 3.4, с. 39);

    К_Нu - коэффициент, учитывающий динамическую нагрузку в зацеплении, для косозубых передач при окружной скорости 0,2 м/с и повышенной твердости К_Нu = 1,0 ([2], табл. 3.6, с. 40)

К_Н = 1,36 × 1,06 × 1,0 = 1,44

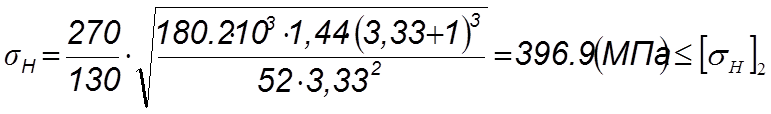
Проверяем отклонение от допустимого значения [s_Н ].

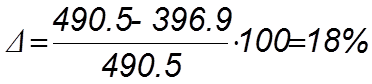, что удовлетворяет условию при малых

габаритах редуктора.

4.6.2 Определяем силы в зацеплении:

Окружная сила

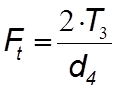                                                       (4.57)

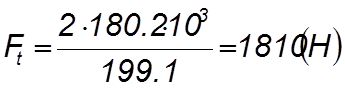
Радиальная сила

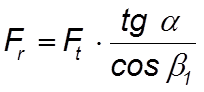                                                  (4.58)

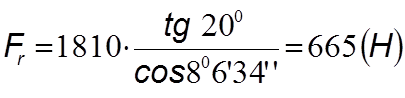
Осевая сила

                                                    (4.59)

4.6.3 Выполняем проверку зубьев на выносливость по напряжениям изгиба ([2], с. 46, ф. 3.25):

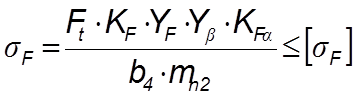                                   (4.60)

где К_F - коэффициент нагрузки;

Y_F - коэффициент, учитывающий форму зуба;

Y_b - коэффициент, учитывающий повышение прочности косых зубьев по сравнению с прямыми;

    К_Fa - коэффициент, учитывающий распределение нагрузки между зубьями

4.6.3.1 Определяем коэффициент нагрузки:

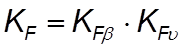                                                   (4.61)

где К_Fb-коэффициент, учитывающий неравномерность распределения нагрузки по длине зуба (коэффициент концентрации нагрузки), при y_bd =1,2 и передаче с нессиметричным расположением колес по отношению к опорам К_Fb = 1,53 ([2], табл. 3.7, с. 43);

K_Fu - коэффициент, учитывающий динамическое действие нагрузки (коэффициент динамичности), для косозубых передач с 8-ой степенью точности, при окружной скорости 0,2 м/с и повышенно твердости
К_Fu = 1,1 ([2], табл. 3.8, с. 39)

4.6.3.2 Коэффициент Y_F зависит от эквивалентных чисел зубьев z_u1 и z_u2 :

Для шестерни

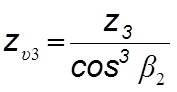                                                     (4.62)

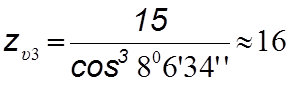
Для колеса

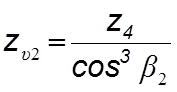                                                     (4.63)

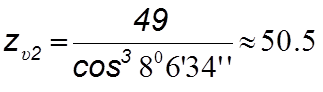
При этом Y_F3 = 4,3 и Y_F4 = 3,659 ([2], с. 42).

4.6.3.3 Определяем допускаемое напряжение

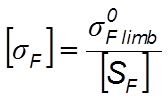                                                     (4.64)

где s⁰_{F lim b}– предел выносливости при отнулевом цикле изгиба, соот-ветствующего базовому числу циклов, для колеса из стали 40ХН при термической обработке- улучшение s⁰_{F lim b2} = 550 МПа, а для шестерни из стадии 40ХН при термической обработке- улучшение s⁰_{F lim b1} = 700 МПа;

    [S_F ] – коэффициент безопасности

Определяем коэффициент безопасности:

                                                (4.65)

где [S_F ]' – коэффициент, учитывающий нестабильность материала зубчатых колес, [S_F ]' = 1,75([2], табл. 3.9, с. 45);

    [S_F ]'' – коэффициент, учитывающий способ получения заготовки зубчатого колеса, для поковок и штамповок [S_F ]'' = 1,0([2], с. 44)

Для шестерни

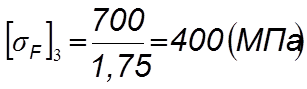
Для колеса

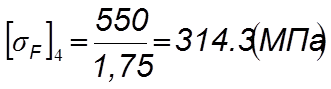
4.6.3.4 Находим отношения

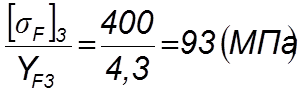                                         (4.66)

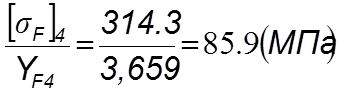                                      (4.67)

4.6.3.5 Дальнейшие расчеты ведем для зубьев колеса, так как для него найденное отношение меньше.

4.6.3.6 Определяем коэффициент Y_b:

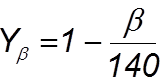                                                     (4.68)

где b - угол наклона делительной линии зуба, b = 8,156

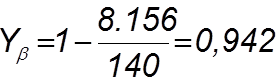
4.6.3.7 Определяем коэффициент К_Fa:

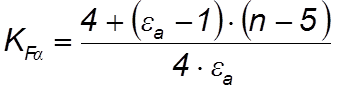                                        (4.69)

где e_а– коэффициент торцового перекрытия, e_а = 1,5;

    п – степень точности колес, п = 8

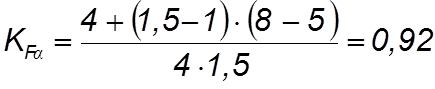
Проверяем зуб колеса по формуле:

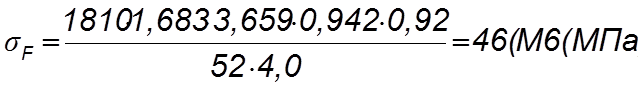
Расчет выполнен правильно, так как s_F < [s_F ] (46 < 490).

4.7 Выполняем проверочный расчет шестерни и колеса первой ступени

4.7.1 Проверяем контактные напряжения:

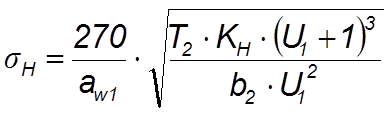                                    (4.70)

где К_Н – коэффициент нагрузки

                            К_Н = К_Нb× К_Нa× К_Нu                  (4.71)

где К_Нb - коэффициент, учитывающий распределение нагрузки по длине зуба, при y_bd = 1,2 и передаче с нессиметричным расположением колес по отношению к опорам К_Нb = 1,36 ([2], табл. 3.5, с. 39);

    К_Нa - коэффициент, учитывающий распределение нагрузки между зубьями, для косозубых передач с 8-ой степенью точности и окружной скоростью 0,2 м/с К_Нa = 1,09 ([2], табл. 3.4, с. 39);

    К_Нu - коэффициент, учитывающий динамическую нагрузку в зацеплении, для косозубых передач при окружной скорости       0,2 м/с и повышенной твердости К_Нu = 1,0 ([2], табл. 3.6, с. 40)

К_Н = 1,36 × 1,09 × 1,0 = 1,48

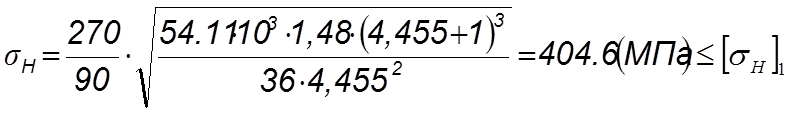
Проверяем отклонение от допустимого значения [s_Н ].

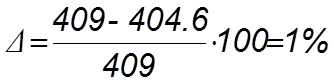, что удовлетворяет условию