Введение в математическое моделирование. Математические методы и моделирование горной промышленности. Количественные методы анализа хозяйственной деятельности, страница 9

Транспортная матрица совмещает матрицу стоимостей и матрицу объемов перевозок. В этой матрице по строкам записаны ограничения по запасам продукции у поставщиков, а поставщика потребности потребителей. В отличии от прочих задач линейного программирования транспортная задача всегда имеет оптимальное решение. При определении оптимального плана перевозок должны выполняться следующие условия.

·  От каждого поставщика должна вывозиться вся продукция, которой он располагает 

x₁₁+x₁₂+…+x_1n=a₁

…

x_m1+x_m2+…+x_mn=a_m

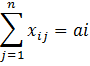
·  Потребности каждого потребителя удовлетворяются полностью

x₁₁+x₁₂+…+x_m1=b₁

…

x_m1+x_m2+…+x_mn=b_n

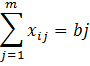
·  Перевозимое количество продукта может быть отрицательным

xij≥0, (j=1…n,i=1…m)

·  Сумма всех затрат по перевозке продукции должна быть минимальной

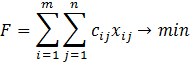
F= c₁₁x₁₁+… +c_1nx_1n+… +c_2nx_2n+… +c_m1x_m1+… +c_m2x_m2+… +c_mnx_mn

Метод потенциалов

Решение транспортной задачи включает два основных этапа:

·  Этап 1

o  Построение опорного решения

o  Расчет системы потенциалов

o  Проверка первоначального плана на оптимальность

·  Этап 2

o  Улучшение плана перевозок

o  Расчет системы потенциалов

o  Проверка улучшенного плана на оптимальность

Второй этап повторяется до получения оптимального решения

Решение задачи

·  Этап 1

o  Построение опорного решения

Для построения мы будем пользоваться методом наименьших стоимостей. Начиная с первого столбца, последовательно заполняются клетки, содержащие наименьшие стоимостные показатели. При этом в клетке проставляется максимально возможный объем перевозок, для чего сопоставляются объемы запасов и потребности. Процедура повторяется до получения допустимого решения, последний столбец заполняется из условия соблюдения ограничений по всем строкам и этому столбцу. План называется опорным, если в нем m+n-1  задействованных клеток. Если число задействованных клеток меньше чем  m+n-1, то построить систему потенциалов нельзя и такой план называется вырожденным. Для решения такой задачи в клетку или клетки без перевозок проставляют фиктивную перевозку малой величины ξ. После этого задачу решают как невырожденную. А в оптимальном плане ξ заменяют нулями.

o  Расчет системы потенциалов

Для того, чтобы допустимый план транспортной задачи был оптимальным необходимо и достаточно, чтобы ему соответствовала система чисел:

U₁, u₂…u_m, v₁, v₂…v_n – которые называются потенциалами.

Система потенциалов в оптимальном плане должна удовлетворять следующим условиям:

1.  v_j-u_i≤c_ij, если x_ij=0

2.  v_j-u_i=c_ij, если x_ij>0 (j=1…n, i=1…m)

vj – потенциал столбца

ui – потенциал строки

c_ij – элемент матрицы затрат опорного плана в пересечении i - ой строки и j – ого столбца.

Расчет системы потенциалов производится на основании условия 2 (v_j-u_i=c_ij, если x_ij>0 (j=1…n, i=1…m))

Для построения системы потенциалов надо задаться потенциалом одного поставщика или потребителя, т.е. строки или столбца. Обычно присваивают нулевой потенциал строке имеющий занятую перевозкой клетку с наибольшей стоимостью.

o  Проверка первоначального плана на оптимальность

Для клеток, незанятых перевозками проверяется выполнение условия 1 (v_j-u_i≤c_ij, если x_ij=0), для этого вычисляют характеристику клетки:

e_ij=v_j-u_i-c_ij

Если e_ij≤0 для всех незанятых клеток, то план оптимален, ели есть положительные превышения, то план может быть улучшен.

·  Этап 2

o  Улучшение плана перевозок

o  Расчет системы потенциалов

o  Проверка улучшенного плана на оптимальность