Введение в математическое моделирование. Математические методы и моделирование горной промышленности. Количественные методы анализа хозяйственной деятельности, страница 4

Если переменные Xj неограниченные, то в процессе решения следует произвести замену Xj на Yi, которые могут принимать только положительные значения. Для этой цели переменные Xj переводятся в базис, а на их место вводятся переменные Yi. Далее система решается относительно вспомогательных переменных Yi, а затем оптимальное решение подставляется в уравнение связи и определяется оптимальные значения исходных переменных Xj. Если переменные X могут принимать только положительные значения или произведена соответствующая замена, то выбор разрешающего столбца и разрешающей строки осуществляется таким образом, чтобы получить опорное, а затем оптимальное решение, используя минимальное число итераций (преобразований симплексной таблицы).

Получение опорного решения:

·  Выбирается строка с отрицательным опорным членом, если среди коэффициентов нет отрицательных, то система ограничений несовместна.

·  Среди отрицательных коэффициентов этой строки выбирается любой столбец, содержащий этот коэффициент и назначается разрешающим.

·  Вычисляются все неотрицательные соотношения   и строка для которой это соотношение минимально назначается разрешающей.

Поиск оптимального решения:

В качестве разрешающего, принимают столбец, содержащий отрицательный элемент Cs в Z строке, максимальный по абсолютной величине, если этот столбец не содержит положительных элементов, то форма неограниченна

Вычисляют все неотрицательные соотношения  и строка, для которой это отношение минимально назначается разрешающей

Если после преобразования в Z строке имеются отрицательные элементы, то это решение неоптимальное и оптимизацию следует продолжить

Геометрический смысл

Геометрически поиск опорного решения представляет собой поиск вершины многогранника ограничений, а поиск оптимального решения направленный перебор вершин многогранника ограничений, при котором возрастает значение целевой функции. Число итераций в симплекс методе зависит от числа вершин, которые встречаются при переходе от базисного решения к опорному, а затем оптимальному.

Пример: Решить задачу графически и численно.

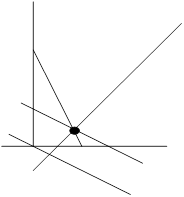
X=4,2 Y=2,3, Zmax=

Решаем задачу численным методом