Введение в математическое моделирование. Математические методы и моделирование горной промышленности. Количественные методы анализа хозяйственной деятельности, страница 8

Транспортная задача линейного программирования

Заключается в определении объемов перевозок от поставщиков к потребителям, если известны объемы выпуска продукции у каждого поставщика и потребности потребителей, а также затраты на перевозку грузов от поставщиков к потребителям. План перевозок должен иметь минимальные затраты. Модель транспортной задачи в общем виде:

Дано: n – потребителей со спросом на однородную продукцию b₁, b₂…b_n и m – поставщиков этой продукции, производительностью a₁, a₂…a_m, C_ijстоимости перевозки единицы продукции от каждого поставщика A_i, до каждого потребителя B_{j ,}  (j=1…n,i=1…m). Требуется составить такой план перевозок: откуда, куда и сколько единиц продукции везти, чтобы все заявки были выполнены, а общие затраты на перевозку продукции были минимальными. В этой постановке задачи не учитываются пропускная способность дорог, транзитная норма, длительность перевозок, запреты, налагаемые на связи между некоторыми пунктами. Если по условию задачи производство продукта во всех пунктах a_i (i=1…m) равно суммарной потребности в этом продукте во всех пунктах b_j (j=1…n).

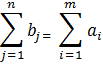
То задача называется закрытой, если это условие не выполняется, то транспортная задача называется открытой. И возможны два варианта:

1.   

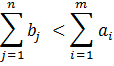
Т.е. производство продукта превышает потребность в нем. Цель задачи состоит в том, чтобы решить у какого из поставщиков и сколько именно продукции следует оставить, обеспечив полностью спрос при минимальных транспортных расходах.

2.   

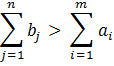
Т.е. потребность в продукте превышает производство. Цель задачи состоит в том, чтобы решить кто из потребителей и сколько именно продукции должен недополучить при условии вывоза всей продукции от поставщиков и минимума затрат на транспортировку.

Любая задача может быть сведена к закрытой путем введения фиктивного поставщика или фиктивного потребителя.

Транспортная задача имеет следующие особенности:

1.  Все ограничения задачи являются равенствами

2.  Каждая переменная входит только в два ограничения

3.  Коэффициенты при переменных в ограничениях равны единице

Благодаря этим особенностям транспортная задача может быть решена более простым методом, чем симплексный метод. Условия закрытой транспортной задачи обычно представляют в виде матрицы: