Переходим к другому примеру, в котором подсчитывались значения полинома второй степени для контрольных точек. В ячейку В2 записываем формулу полинома без абсолютных адресных ссылок, но с учетом множества значений аргумента х.
В2: =C2*A2:A10^2+D2*A2:A10+E2
После ввода формулы выделяем диапазон ячеек В2:В10; щелкаем мышью в строке формул и нажимаем сочетание клавиш Ctrl+Shift+Enter (рис.1.22).
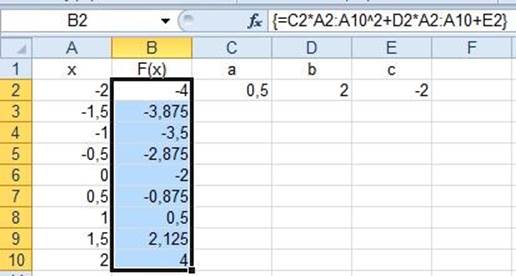
Рисунок 1.22 Подсчет значений функции по формуле массива
Формула массива может оказать неоценимую услугу в деле решения систем линейных алгебраических уравнений практически любой размерности. Для этого в арсенале встроенных функций табличного процессора имеются следующие функции:
− МОБР – возвращает значения обратной матрицы по отношению к исходной; − МУМНОЖ – возвращает результат умножения векторов и матриц.
Следует заметить, что обе функции чётко поддерживают правила векторно-матричной алгебры. Например, обратная матрица может быть найдена только для квадратной двухмерной матрицы. Размерность результата векторного умножения следующая: число строк результата соответствует числу строк первого сомножителя, а число столбцов у результата равно числу столбцов второго сомножителя.
Таким образом, в табличном процессоре Excel есть все возможности решить векторноматричным способом любую линейную систему вида 𝐴 ∙ 𝑋 = 𝐵. Соответственно решение нужно искать по формуле 𝑋 = 𝐴–1 ∙ 𝐵, т.е. обратную матрицу левой части системы нужно умножить на вектор правой части.
Дана следующая система линейных алгебраических уравнений:
x1 +2x2 +3x3 =9
2x1 +4x2 −x3 =11
3x1 +4x2 +2x3 =18
В ячейках электронной таблицы расположим матрицу коэффициентов левой части системы и вектор правой части (рис.1.23). В ячейку А7 вводим формулу: =МОБР(A2:C4). Выделяем диапазон ячеек А7:С9, щелкам в строке формул и нажимаем Ctrl+Shift+Enter. Получили обратную матрицу.
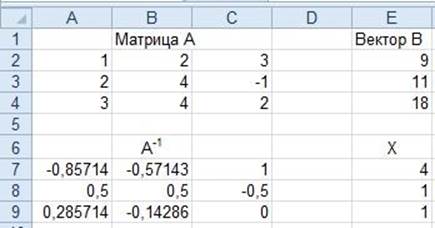
Рисунок 1.23 Решение системы линейных алгебраических уравнений
Переходим к умножению матриц. В ячейку Е7 вводим формулу: =МУМНОЖ(A7:C9;E2:E4),
–1 – вектов которой первый массив соответствует диапазону ячеек обратной матрицы (А ), второй ру В. Выделяем диапазон ячеек Е7:Е9, щелкаем в строке формул и нажимаем сочетание клавиш Ctrl+Shift+Enter. Получили результирующий вектор переменных Х.
Табличный процессор Excel способен обнаружить ошибки в формулах. Он может даже исправить ошибку, если это касается, например, не закрытия скобок в конце формулы. Но в большинстве случаев на видимом уровне ячейки с формулой появляется одна из следующих записей:
§ #ДЕЛ/0! Означает попытку совершить операцию деления на ноль;
§ #ИМЯ? Означает, что табличному процессору неизвестен хотя бы один элемент в составе формулы, например, название подпрограммы-функции;
§ #Н/Д Означает, что при подсчете формулы не хватает данных;
§ #ПУСТО! Ошибка появляется, когда задано пересечение двух диапазонов ячеек, которые в действительности не имеют общих ячеек;
§ #ЧИСЛО Означает, что в формуле возникла проблема со значением, например, вследствие несоответствия аргумента функции;
§ #ССЫЛ! Ошибка появляется, когда используется недопустимая ссылка на ячейку; например, когда ячейка, на которую ссылается формула, удалена;
§ #ЗНАЧ! Означает, что используется недопустимый тип аргумента.
Формулы могут возвращать значение ошибки и в том случае, когда ссылаются на ячейку, которая уже содержит ошибку. Получается так называемый волновой эффект: одна единственная ячейка, содержащая ошибку, может повлиять на множество ячеек, в которых расположены зависимые от этой ячейки формулы.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.