Однако в практике вычислений достаточно часто встречаются зависимости, у которых есть хотя бы один параметр, т.е. некоторая константа. Всем хорошо известен канонический полином второй степени или квадратное уравнение: 𝐹(𝑥) = 𝑎 ∙ 𝑥2 + 𝑏 ∙ 𝑥 + 𝑐. Здесь а, b и с – это параметры. Пусть необходимо повторять расчеты, оперативно изменяя значения переменной х.
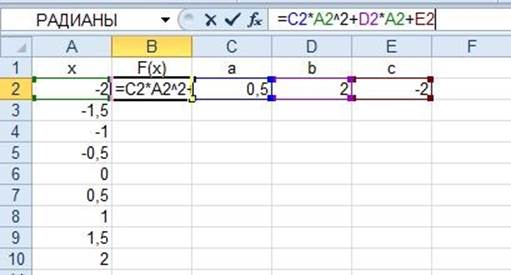
Рисунок 1.19 Формула полинома второй степени с параметрами
В первом столбце покажем значения аргумента х. Во втором столбце будем подсчитывать значения полинома, а параметры расположим в отдельных ячейках. На рисунке 1.19 хорошо видно, как введенная формула (ячейка В2) ссылается на ячейки с параметрами и на значение аргумента х. Если просто скопировать формулу в ячейку В3, то результат расчетов будет нулевым, т.к. согласно принципу относительности значения параметров будут взяты из ячеек справа на один, два и три шага соответственно (ячейки С3, D3 и Е3). Но они являются пустыми. Следовательно, нужно каким-то образом закрепить адреса ячеек с параметрами. Это можно сделать с помощью абсолютного адреса.
Абсолютным называется адрес, который не перемещается в процессе копирования формулы. Признак абсолютности – знак доллара ($). Его можно проставить либо вручную, либо с помощью функциональной клавиши F4.
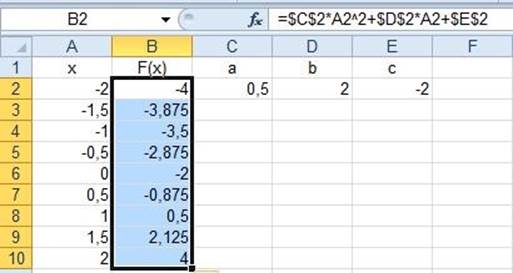
Рисунок 1.20 Формула полинома с абсолютной адресацией
Для записанной в ячейке В2 формулы подводим курсор мыши (в строке формул) к адресу каждого параметра и нажимаем F4. Результат представлен на рисунке 1.20. Теперь можно копировать формулу по столбцу вниз.
Следует заметить, что знаки доллара для адреса каждого параметра проставлены и по строке и по столбцу. Это явно избыточно, т.к. достаточно было бы иметь знак доллара только перед номером строки, который остановил бы перемещение при копировании вниз. Копирования вправо или влево здесь нет; поэтому знаки доллара перед именем столбца избыточны. Но один раз нажать клавишу F4 всё-таки проще, чем каждый раз выбирать нужную позицию для знака доллара.
Формула массива – это такая формула, результатом которой является множество значений. Однако ячейка, в которую введена такая формула, не может разместить все числа; поэтому они поступают в специальный буфер табличного процессора. Их оттуда нужно извлечь и поместить в диапазон ячеек, который полностью соответствует размерности результата. Делается это следующим образом:
− в активную ячейку вводим формулу, которая рассчитывает некоторое множество чисел;
− выделяем диапазон ячеек под будущий результат, начиная с ячейки с формулой;
− активируем формулу щелчком мыши в строке формул;
− выпускаем данные из буфера нажатием сочетания клавиш Ctrl+Shift+Enter.
В результате для всех ячеек выделенного диапазона формула преобразовалась в формулу массива. Об этом свидетельствует тот факт, что формула в строке формул получила фигурные скобки (математический знак для записи векторов и матриц).
Результаты, полученные по формуле массива, являются единым целым; с каждым из них в отдельности нельзя производить какие-либо действия. Например, нельзя удалить данные из отдельных ячеек, нельзя редактировать формулу для отдельной ячейки и так далее. Все эти действия могут производиться только для всего диапазона ячеек, в которых размещены результаты работы формулы массива.
Рассмотрим множественные расчеты по формуле массива для тех же примеров, что были представлены в разделе о копировании формул. Для примера с суммированием данных в ячейку С2 вводим формулу, в которой в качестве слагаемых рассматриваются диапазоны ячеек х и у.

Рисунок 1.21 Расчет по формуле массива
После ввода формулы в ячейку С2 выделяем диапазон ячеек С2:С5; щелкаем мышью в строке формул и нажимаем сочетание клавиш Ctrl+Shift+Enter (рис.1.21).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.