Внутрь функции тангенса следует встроить функцию РАДИАНЫ. Поэтому, находясь в окне функции TAN, вновь обращаемся к «Конструктору» и высвечиваем список ранее использованных функций. Функция РАДИАНЫ есть (рис.1.15).
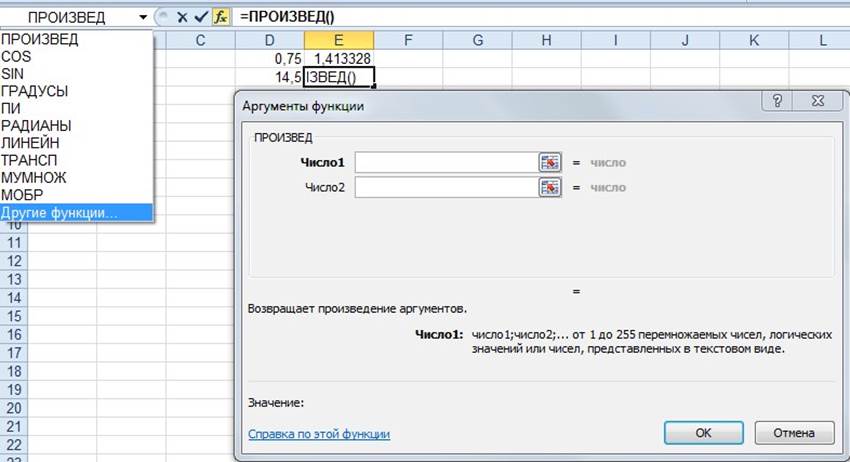
Рисунок 1.14 Ввод функции верхнего уровня и переход на следующий уровень
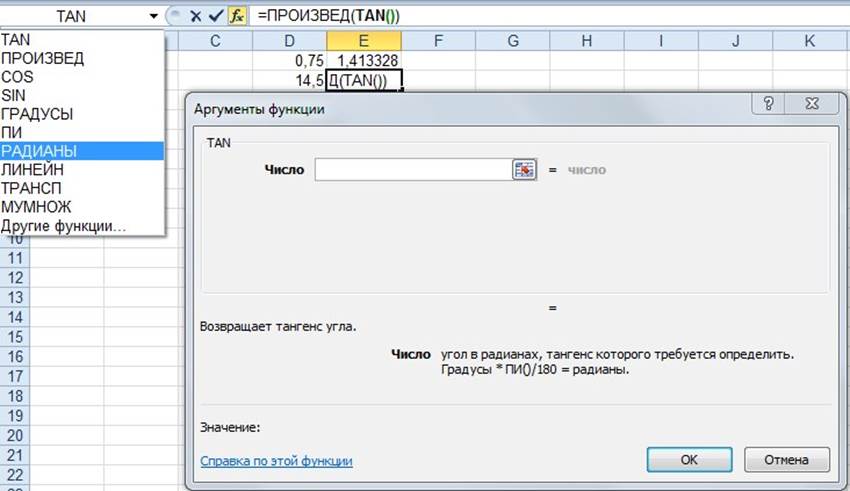
Рисунок 1.15 Переход к очередному ниже расположенному уровню
Вызываем функцию РАДИАНЫ. Открывается диалоговое окно этой функций, в котором в качестве аргумента устанавливаем адрес ячейки со значением дифферента (ячейка D2); при этом целесообразно использовать указатель мыши.
Ещё раз подчеркнем, что нажимать кнопку «ОК» не рекомендуется! Это приведет к сохранению формулы. Напротив, нам необходимо подняться внутри формулы на уровень выше. Это можно сделать простым щелчком мыши в строке формул по той функции, к которой пользователь хочет перейти. Так как функция тангенса нас больше не интересует, то переходить следует к функции ПРОИЗВЕД. Не покидая диалоговое окно функции РАДИАНЫ, щелкаем мышью в строке формул прямо по функции ПРОИЗВЕД (рис.1.16).
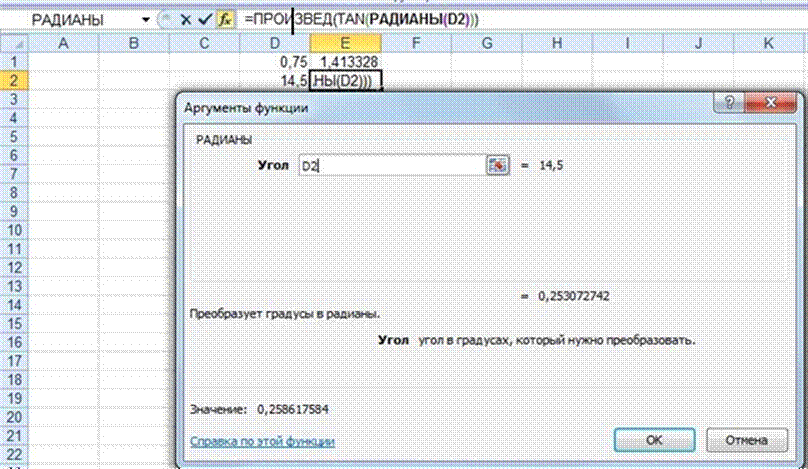
Рисунок 1.16 Переход на верхний уровень вложенности функций
После этого автоматически откроется диалоговое окно функции ПРОИЗВЕД. Переходим к строке «Число 2» и записываем в него адрес суммы синуса и косинуса угла крена (ссылка на ячейку Е1). Заметим, что в строке «Число 1» записаны все необходимые элементы для определения тангенса угла дифферента (рис.1.17).
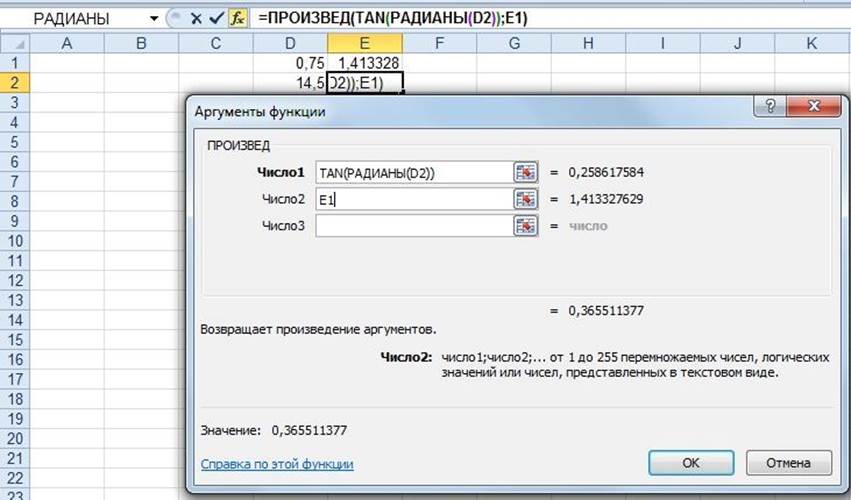
Рисунок 1.17 Заполнение аргументов верхнего уровня
Теперь можно нажать «ОК», т.к. ввод всех необходимых функций и аргументов закончен. На внешнем уровне ячейки Е2 можно прочитать результат вычислений.
Под множественными вычислениями, как правило, понимают получение результата по одной основополагающей формуле, но для различных значений аргумента. Характерным примером в этом случае будет создание таблицы значений функции. Это можно выполнить двумя способами: 1. копированием формулы для всех значений аргумента,
2. созданием формулы массива.
Каждый из способов имеет свои положительные стороны и недостатки. Нельзя дать единых рекомендаций на все случаи жизни. Поэтому разберем каждый из способов подробно.
До настоящего момента ничего не было сказано о том, как видит формулу табличный процессор. Если человек видит её в строке формул с точки зрения функций, операторов и ссылок на ячейки через их адреса (например, А1 или В2), то табличный процессор относится к ссылкам несколько иначе. Ссылка для него представляет шаги, которые необходимо сделать по строкам и столбцам.
Рассмотрим такой пример. Заданы значения переменных х и у. Нужно найти сумму каждой пары значений: А = х + у. Записываем в столбцах исходные данные (рис.1.18) и в ячейку С2 вводим формулу суммирования для первой пары: =А2+В2. Из рисунка видно, что первое слагаемое (окантовка синим цветом) находится в двух шагах влево от ячейки с формулой, а второе слагаемое (окантовка зеленым цветом) – в одном шаге слева. Для ячейки С3 эти же позиции шагов будут повторяться. В этом состоит главный принцип электронных таблиц – принцип относительности адреса. Если из ячейки С2 скопировать формулу в ячейку С3, то она сложит данные для второй пары аргументов х и у (два шага влево плюс один шаг влево).
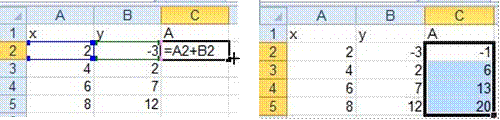
Рисунок 1.18 Копирование формулы
Наиболее удобным способом копирования формулы считается использование маркера «Автозаполнения», который находится в правом нижнем углу активной ячейки (черный квадрат). Пусть будет активной ячейка С2. При подходе указателя мыши к маркеру «Автозаполнения» (рис.1.18), он преобразуется в «малый крест». Зажимаем левую клавишу мыши и двигаемся вниз. Происходит автоматическое копирование формулы с одновременным показом результата.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.