Лекции по нелинейным системам, страница 8

1.  Критерий Гурвица.

Алгебраический критерий. Надо построить матрицу Гурвица и подсчитать ее определители.

2.  Критерий Михайлова.

Используется годограф замкнутой системы (всей системы целиком).

3.  Критерий Найквиста.

Используется годограф на комплексной плоскости для разомкнутой системы (размыкается единичная обратная связь). По состоянию устойчивости разомкнутой системы судим об устойчивости замкнутой системы.

           

Рассмотрим систему 2-го порядка:

Преобразуем в нормальную форму Коши: ,

Для простоты примем

Тогда: 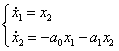 , откуда получаем дифференциальное уравнение:

, справедливое при

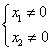
Неопределенность возникает в случае, если 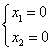- особая точка (для линейных систем возможна только одна точка – точка равновесного состояния).

Для нелинейных систем возможно появление не только точек, но и линей неопределенностей.

Характеристическое уравнение:

Корни характеристического уравнения:

Рассмотрим 6 возможных вариантов:

1)  Корни чисто мнимые.

2)  Корни комплексные с отрицательной вещественной частью.

3)  Корни комплексные с положительной вещественной частью.

4)  Корни вещественные и отрицательные.

5)  Корни вещественные и положительные.

6)  Корни вещественные с разными знаками.

 

1.  Чисто мнимые корни.

, при

В этом случае мы получаем границу устойчивости