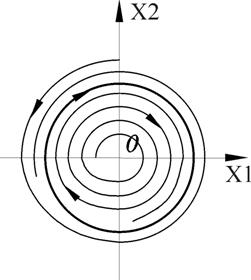
Рисунок 11 – Автоколебания
Метод припасовывания используется только для кусочно-линейных систем (нелинейность разбивается на ряд линейных участков). Уравнение состояния разбивается на линейные дифференциальные уравнения для различных участков динамического процесса, далее они решаются в общем виде на каждом линейном участке, затем определяются коэффициенты решения в конце начального участка, которые принимаются за начальные значения для следующего участка.
Основной недостаток: сложно увязывать переходы от одного участка к другому.
Пример:
Сухое трение: ![]() Рассматриваются 2 линейных
участка.
Рассматриваются 2 линейных
участка.
Метод точечного преобразования – усовершенствованный метод припасовывания с использованием фазового пространства. Как следствие, легче осуществляется переход от одной области (участка) к другой.
а) Линеаризация вблизи рабочей точки (метод касательной линеаризации).
б) Метод гармонической линеаризации.
в) Метод статистической линеаризации.
г) Комбинированные методы.
Линеаризация вблизи рабочей точки (метод касательной линеаризации).
Предполагаются малые отклонения относительно рабочей точки и нелинейные характеристики заменяются эквивалентными линейными. При этом характеристики бывают как статические, так и динамические.
Основной недостаток: метод используется только при малых сигналах (т.е. отклонениях). При этом нелинейные характеристики также должны быть непрерывны и дифференцируемы в окрестности данной точки (хотя бы один раз).
В основном, используется для оценки устойчивости системы вблизи рабочей точки и оценки статических ошибок.

Если нелинейная функция f является аналитической, т.е. непрерывной и бесконечно дифференцируемой в рабочей точке, то она может быть разложена в ряд Тейлора. Для малых приращений можно отбросить члены высших порядков.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.