2. 
, 
, 
,
, 
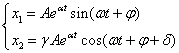
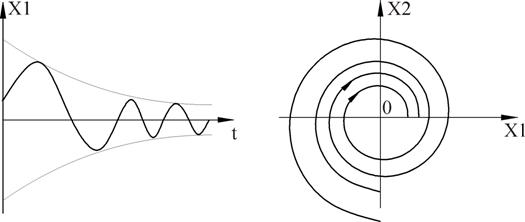
Рисунок 19 – Фазовый портрет и переходный процесс
Фазовый портрет представляет собой логарифмическую спираль, сходящуюся к нулю.
Точка (0,0) – особая точка типа «устойчивый фокус».
3. , 
, ,
,
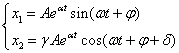
Фазовый портрет представляет собой логарифмическую спираль, рассходящуюся от нулю.
Рисунок 20 - Фазовый портрет и переходный процесс
Точка (0,0) – особая точка типа «неустойчивый фокус».
4. 
, 
|
Рисунок 21 – Фазовый портрет |
Рисунок 22 – Переходные процессы |
Асимптоты: 
, 
Точка (0,0) – особая точка типа «устойчивый узел».
Вырожденный случай получаем, когда корни одинаковы.
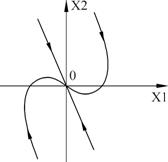
Рисунок 23 - Вырожденный устойчивый узел
Точка (0,0) - особая точка типа «вырожденный устойчивый узел».
Если матрица в уравнении Коши имеет диагональный вид, то фазовый портрет имеет вид
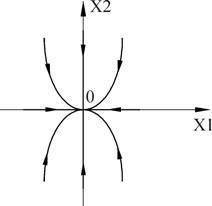
Рисунок 24 – Частный случай фазового портрета системы
Если матрица имеет диагональный вид и корни равны, то имеем случай
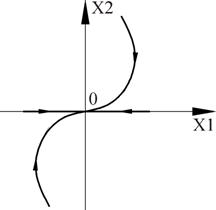
Рисунок 25 - Частный случай фазового портрета системы
5. , 
|
Рисунок 26 – Фазовый портрет |
Рисунок 27 – Переходный процесс |
Точка (0,0) - особая точка типа «неустойчивый узел».
Вырожденный случай получаем, когда корни одинаковы.
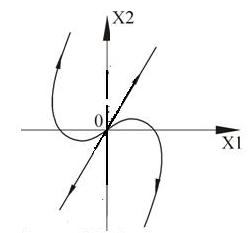
Рисунок 28 – Вырожденный неустойчивый узел
Если матрица в уравнении Коши имеет диагональный вид, то фазовый портрет имеет следующий вид
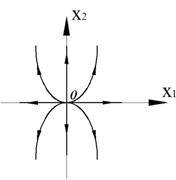
Рисунок 29 - Частный случай фазового портрета системы
Если матрица имеет диагональный вид и корни равны, то имеем случай на рис. 35
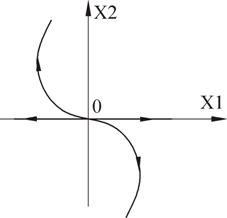
Рисунок 30 - Частный случай фазового портрета системы
6. , 
Кривые – гиперболы
|
Рисунок 31 – Фазовый портрет |
Рисунок 32 – Переходный процесс |
Точка (0,0) - особая точка типа «седло».
Если матрица А имеет диагональный вид, то фазовый портрет изменится следующим образом.
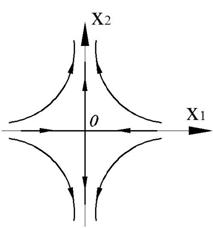
Рисунок 33 - Частный случай фазового портрета системы
Для уточнения фазовых траекторий используется метод изоклин.
Изоклина – это линия, соединяющая точки фазовых траекторий с одинаковым наклоном касательных. Для линейных систем изоклины представляют собой прямые и проходят через точку (0;0).
Изоклина определяется следующим образом:
Рисунок 34 – Уточнение фазового портрета методом изоклин
Фазовые портреты нелинейных систем.
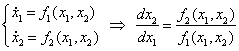
Неопределенность:
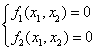
В отличие от линейных систем, в нелинейных системах могут быть и особые линии.
Особые точки те же: центр, узел, фокус, седло и т.д.
Особые линии: устойчивый предельный цикл (фазовая траектория замкнута), неустойчивый предельный цикл, линия устойчивого положения, сепаратрисса (линия, разделяющая области с разным видом фазовых траекторий) и т.д.
Для выявления вида особых точек уравнение системы линеаризуется в их окрестности, определяются корни характеристического уравнения линеаризованной системы.
Уравнение
изоклин: 
Типовые случаи фазовых портретов нелинейных систем.
1. Устойчивый предельный цикл (автоколебания).
Фазовая траектория стремится к предельному циклу, следовательно, цикл устойчив.
|
Рисунок 35 – Фазовый портрет |
Рисунок 36 – Переходный процесс |
В данном случае система неустойчива в малом (точка (0;0) – неустойчивый фокус), но устойчива – в большом. Т.е. в малых значениях она будет расходиться, а при больших начальных условиях
2. Неустойчивый предельный цикл.
|
Рисунок 37 – Фазовый портрет |
Рисунок 38 – Переходный процесс |
Система в малом становится устойчивой (точка (0;0) – неустойчивый фокус), а в большом – неустойчивой.
Практически, неустойчивый предельный цикл ограничивает область начальных условий, в пределах которой система устойчива.
3. Несколько предельных циклов.
|
Рисунок 39 – Фазовый портрет |
Рисунок 40 – Переходный процесс |
Внешний предельный цикл устойчив, внутренний – неустойчив.
4. Сепаратриcса.
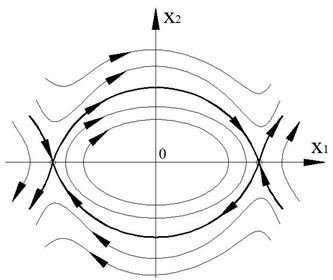
Рисунок 41 – Особая линия типа «сепаратриса»
Сепаратрисcа – особая линия, разделяющая области с различным видом фазовых траекторий.
Три особых точки: «центр» и две типа «седло». Всего на фазовой плоскости образовано 5 областей.
5. Отрезок установившихся состояний (отрезок покоя).
Фазовая траектория только входит в отрезок покоя. На отрезке скорость равна нулю (покой).
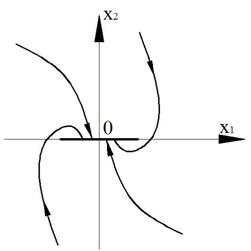
Рисунок 42 – Особая линия типа «отрезок покоя»
6. Скользящий процесс.
Рисунок 43 – Скользящий процесс
Если траектория приходит не на отрезок AB, то она преломляется на линии скользящего процесса и затем возвращается на отрезок.
При попадании на отрезок скользящего процесса, система начинает двигаться по линии скользящего процесса в направлении точки (0,0)
Практическое значение: в данном случае мы получаем желаемый переходный процесс с заданным законом движения. Это достижимо, если организовать соответствующее управление (нелинейный закон управления), что возможно далеко не всегда.
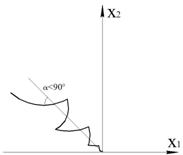
Рисунок 44 – Движение по линии скользящего процесса
В результате получаем процесс движения по отрезку скользящего процесса в виде колебаний относительно отрезка с амплитудой, стремящейся к нулю, и частотой, стремящейся к бесконечности.
7. Линия переключений (нелинейный закон управления).
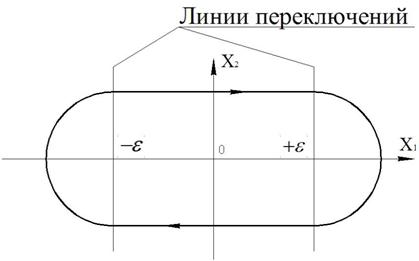
Рисунок 45 – Фазовый портрет системы
Пример. Построить фазовый портрет для системы, описываемой следующими уравнениями:
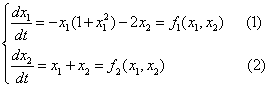
Условие 
не
выполняется, следовательно направление фазовых траекторий может быть
произвольным.
Разделим уравнение (2) на уравнение (1), получим дифференциальное уравнение фазовой траектории:
Особые точки и линии: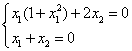 
Решение дает 3 особые точки:
1) 
2)
3) 
Для определения типа особых точек необходимо линеаризовать уравнение нелинейной системы в окрестности этих особых точек:
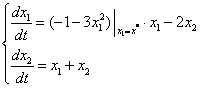
Далее символ
подразумевается,
но не пишется.
1)
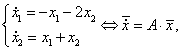
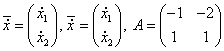
Для определения типа особой точки
решаем характеристическое уравнение:
В итоге получаем чисто мнимые корни. Особая точка типа «центр» (фазовая траектория – эллипсы).
2)
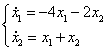
Корни вещественные, разного знака. Особая точка типа «седло».
Асимптоты:
, k – коэффициент наклона асимптоты
Асимптоты действительны только в малой окрестности точки (1;-1)
3)
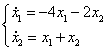Далее
аналогично пункту 2)
Определим направление фазовых
траекторий: возьмем точку 
и подставим в
исходное нелинейное уравнение системы: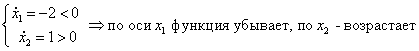 
Изоклины:
при с =1 (наклон касательной 45о): 
, изоклина пройдет через все особые
точки.
Таким образом, получаем фазовый портрет
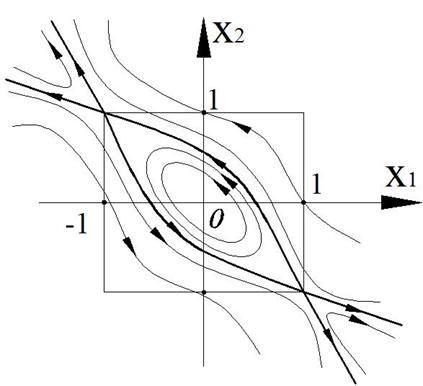
Рисунок 46 – Фазовый портрет
Изображение переходных процессов на фазовой плоскости на примере электромеханического следящего привода.
|
|
ДПТ – двигатель постоянного тока ДС – датчик скорости ДП - датчик положения
|
Рисунок 47 – Структурная схема электромеханического следящего привода
Будем считать, что характеристики ДС и ДП линейные.
Пример 1. Следящий привод. Нагрузка: инерционная и вязкое трение.
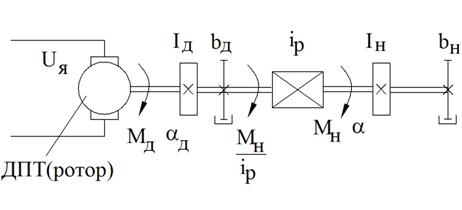
Рисунок 48 – Структурная схема механической части объекта
-
момент инерции двигателя
-
момент инерции нагрузки
-
передаточное отношение редуктора
-
вязкое трение нагрузки
-
коэффициент противоЭДС
-
коэффициент усиления по моменту
-
уравнение ДПТ
Введем допущение: в рабочем
режиме ДПТ
(в реальной жизни – гистерезис)
Введем допущение: пренебрегаем
электрической постоянной двигателя (
на два порядка
меньше, чем электромеханическая постоянная).
Уравнение моментов, приведенных к валу двигателя:
,
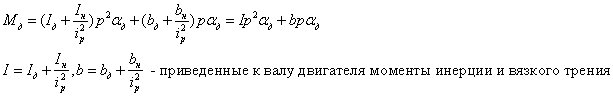
где
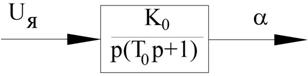
Рисунок 49 – Объект управления
- описание объекта управления
(интегрирующее звено с запаздыванием)
Необходимо найти уравнение регулятора:
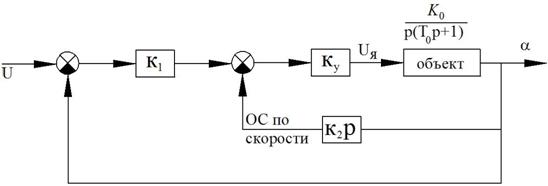
Рисунок 50 – Пропорциональный интегральный регулятор
Обратная связь по скорости математически представлена верно, но на практике так делать нельзя из-за шумов (при дифференцировании не будет асимптоты).
При моделировании для исключения шумов необходимо изменить схему следующим образом:
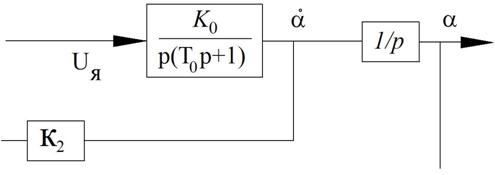
Рисунок 51 – Изменения в схеме для моделирования
Уравнение регулятора с усилителем:
, 
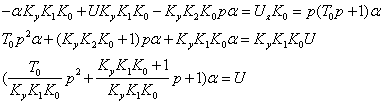
- колебательное звено.
Обозначим: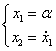 
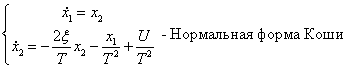
Фазовые портреты при U=0
1)
0<
<1
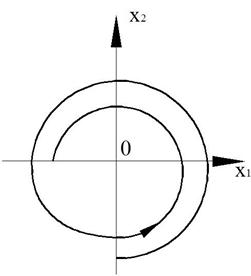
Рисунок 52 – Фазовый портрет (случай 1)
2)
=0
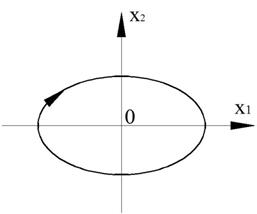
Рисунок 53 – Фазовый портрет (случай 2)
3)
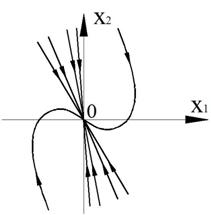
Рисунок 54 – Фазовый портрет (случай 3)
При 
фазовые портреты
соответственно трем случаям имеют следующий вид:
|
|
|
|
Рисунок 55 – Фазовые портреты для случаев 1, 2 и 3 при
Рисунок 56 – Переходные процессы (случай 1 и 3)
Пример 2. Следящий привод. Нагрузка: инерционная, вязкое и сухое трение.
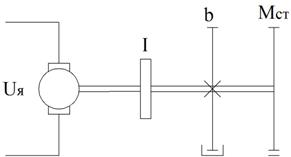
Рисунок 57 – Структурная схема механической части объекта ( все приведено к валу двигателя)
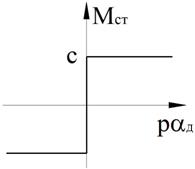
Рисунок
58 – Вид нелинейности 
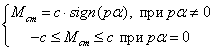
Возможны два случая:
(прохождение
через «0» скорости – тело движется)
при 
при 
Рассмотрим
случай 
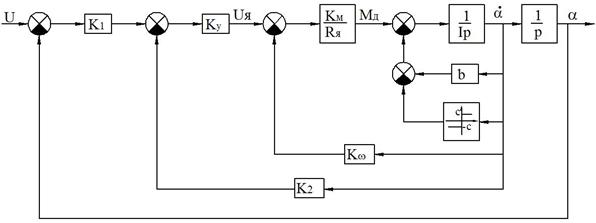
Рисунок 59 – Структурная схема системы
В случае остановки появится новый элемент:
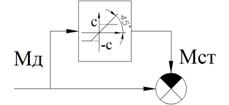
Рисунок 60 – Элемент структурной схемы
Рассмотрим случай, когда входное воздействие U=0
1) Движение есть
Справедливо,
если 
или ,
но 
2) Покой
В данном случае появляется «отрезок покоя»
Вне отрезка зоны покоя:
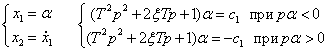
а) 
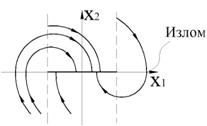
Рисунок 61 – Фазовый портрет системы (случай а)
Система устойчива, колебания затухают. Особая линия типа «отрезок покоя».
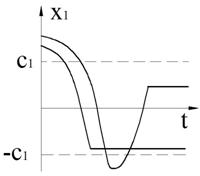
Рисунок 62 – Типовые переходные процессы в системе (случай а)
б) 
- особая точка
типа «устойчивый узел»
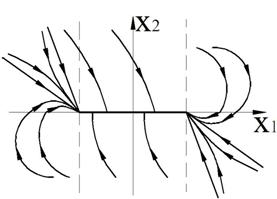
Рисунок 63 – Фазовый портрет системы (случай б)
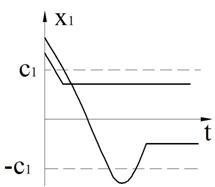
Рисунок 64 – Типовые переходные процессы
Пример 3. Следящая система. Нагрузка чисто инерционная. Бесконечно большой коэффициент усиления усилителя.
Рисунок 65.
В предыдущем примере: Теперь объект представляет собой двойной интегратор:
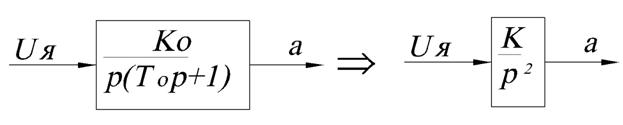
Рисунок 66.
Уравнения системы получены по структурной схеме.
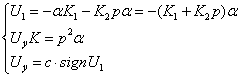
Объединяем в одно уравнение:
Переходим к форме Коши:
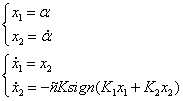
Особая точка: 
Особая линия :
- линия
переключений
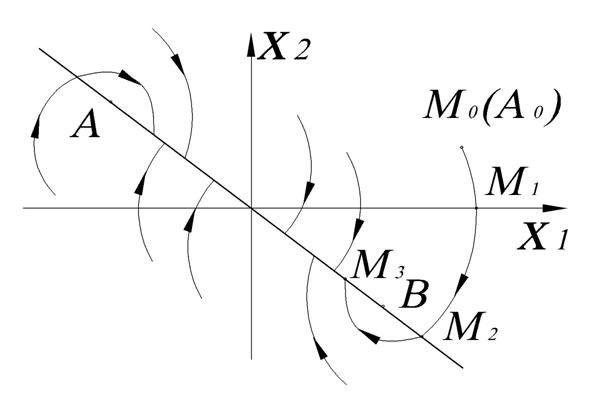
Рисунок 67.
Фазовые траектории являются параболами.
1) Выше
линии переключений 
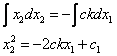
Параболы симметричны относительно Ох1
2) Ниже
линии переключений 
АВ- отрезок скольжения
При попадании на линию переключения и на отрезок скользящего процесса, изображающая точка стремиться к точке (0,0) по линии переключения (по отрезку скользящего процесса). При этом, теоретически, частота колебаний стремиться к бесконечности, а амплитуда к нулю.
Условия возникновения скользящего процесса:
Фазовые траектории должны входить с двух сторон в линию переключения под углом <90° относительно отрезка с точкой установившегося состояния.
Уравнения движения в скользящем процессе:
Нелинейные системы 2-го порядка на участке скольжения вырождается в линейную систему 1-го порядка, причём закон движения на зависит от параметров системы, а зависит от коэффициентов управления К1 и К2. В общем случае порядок системы понижается на 1.
Переходный процесс:
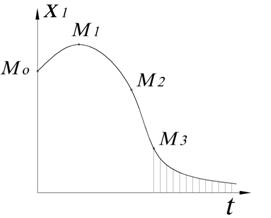
Рисунок 68.
Определение координат отрезка скользящего процесса:
Линии фазовой траектории- параболы. Значит в точках А и В касательные к параболам должны совпадать с линией переключения.
- тангенс угла наклона
касательной
Подставляем в уравнение фазовых траекторий:
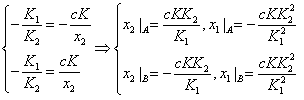
Используется для нелинейных систем, где нелинейность кусочно-линейная и для каждого участка можно найти общее решение.
Процедура: Ищется общее решение дифференциального уравнения на каждом участке, далее происходит состыкование начальных и конечных условий для двух соседних участков, т.е. определяются коэффициенты дифференциальных уравнений.
Пример:
Система управления сушильного шкафа. Цель: поддерживать постоянную температуру в шкафу. Заданная температура задаётся подбором резисторов.
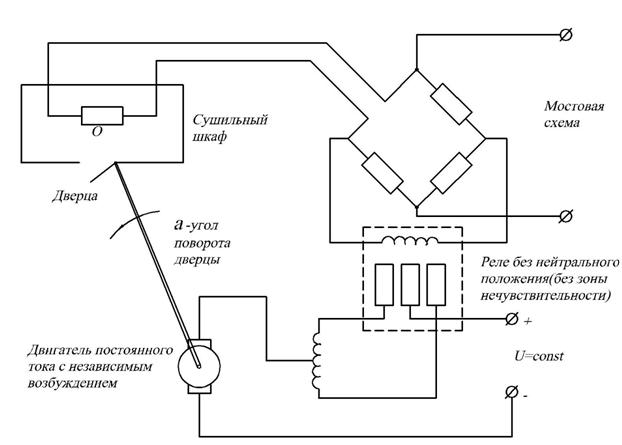
Рисунок 69.
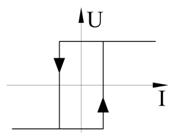
Рисунок 70. Реле.
Это реле без среднего центрального положения, т.е. без зоны нечувствительности.
Изменения температуры θ приводит к появлению тока I, что приводит к замыканию реле. Напряжение U=const подаётся на соответствующую обмотку электродвигателя, который открывает, либо закрывает заслонку.
Допущения:
Считаем, что процесс изменения
температуры медленный, тогда возникающий ток пропорционален изменению
температуры. Тогда скорость вращения двигателя 
пропорциональна
напряжению U.
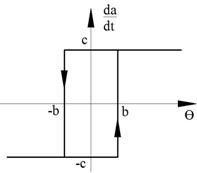
Рисунок 71.
Уравнение объекта – чистая инерционность
|
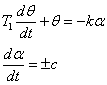
АВ:
BD:
|
Рисунок 72. |
|
Уравнение для участка AB:
Проинтегрируем:
Для простоты примем, что при t=0 мы находимся в точке А.
Н.У.: t=0,
|
Рисунок 73. |
|
Уравнение для участка BD:
|
Рисунок 74. |
Определим значение в конечной точке для участка AB (t=
)
Условие возникновения автоколебаний, период АВD:
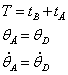
Если существует такое положительное и вещественное T, то существует периодическое решение. Если это решение устойчивое, то возникают автоколебания.
Недостаток метода: сложно увязывать начальные и конечные условия каждого участка.
Является усовершенствованным методом припасовывания.
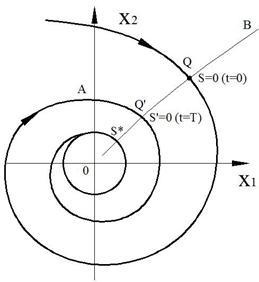
Рисунок 75.
Q: S(t=0)
Q’: S’(t=
)
S' =f(S)- функция последования, определяет закон точечного преобразования.
Система не идёт по дуге AB, она её пересекает.
Определение последующих точек по исходным на отрезке АВ называется точечным преобразованием отрезка АВ в самого себя.
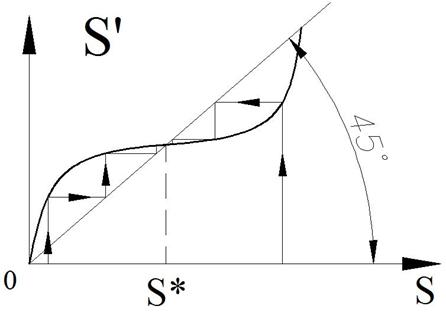
Рисунок 76.
При S’=S=S* получаем периодическое решение (предельный цикл), т.е. получаем точечное преобразование точки Q в саму себя. Диаграмма точечного преобразования – графическое представление функции последования.
По S находим S’, S’ принимаем за новое S, по S находим новое S’ и так далее.
В точку S* можно придти как слева, так и справа, т.к. в данном случае устойчивое автоколебание.
Данная процедура эквивалентна увязыванию начальных и конечных условий метода припасовывания.
- условие возникновения
автоколебаний.
Неустойчивый предельный цикл.
|
Рисунок 78. |
Рисунок 77. |
|
|
Рисунок 80. |
Рисунок 79. |
|
Два предельных цикла
|
Рисунок 82. |
Рисунок 81. |
|
Рисунок 84. |
Рисунок 83. |
Расходящиеся колебания.
|
Рисунок 86. |
Рисунок 85. |
Недостаток метода: сложно найти S’=f(S), поэтому чаще её находят в параметрической форме
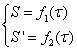
- время перехода из точки 
в 
.
Устойчивый предельный цикл.
|
Рисунок 87. |
|
Неустойчивый предельный цикл.
|
Рисунок 88. |
|
Пример: Сушильный шкаф (условия и схема аналогичны примеру, рассмотренному ранее)
|
Рисунок 89. |
|
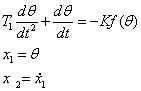
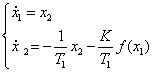
Наша задача – найти условия возникновения автоколебаний.
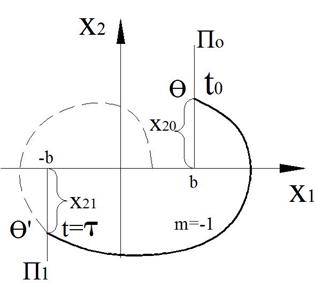
Рисунок 90.
Ввиду нечёткой симметрии функции f(x1), точечное преобразование прямой
можно рассматривать как точечное
преобразование в 
,
а не в .
На участке θθ’ f(x1)=с
Решение будем искать в
параметрической форме. Обозначим: θ и θ’ как 
и
что является параметрической записью функций последования. 
и 
-
ординаты точек Q и Q’.
В точке Q: t=0
-начальные условия
Подставим эти значения в уравнение
В точке Q’:
t= 
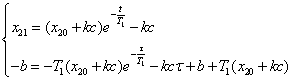
Диаграмма точечного преобразования
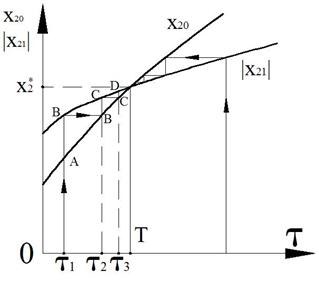
Рисунок 91.
- время переходов
из точки в точку
·
Так как функция величина
отрицательная (на полупрямой), рассматриваем 
· Процесс сходится
·
Параметры автоколебаний 
и
T (полупериод)
·
Рассматриваем процесс из точки А-В-С-D и построим переходные процессы по 
и
, то есть по 
и
(изменение температуры и скорость
изменения температуры)
Переходный процесс по этой диаграмме:
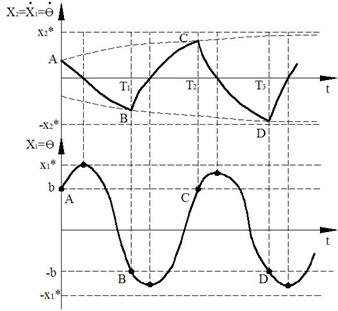
Рисунок 92.
Переходные процессы были
нарисованы для случая, когда начальная точка 
.
Система стремится к предельному циклу с параметрами 
и
. Аналогично можно построить
переходные процессы если 
(извне
предельного цикла). В этом случае система будет стремиться к тем же параметрам,
но с другой стороны. Исключив время, можно построить фазовый портрет и мы
получим устойчивый предельный цикл (автоколебания).
С целью экономия электроэнергии можно использовать электрореле с зоной нечувствительности, но это приведёт к появлению зоны покоя (участок с неконтролируемой температурой), это допустимо, если заданы допуски температуры (интервал ошибки).
Используется для определения предельных циклов (практическое значение имеет получение автоколебаний). Так же используется для изучения устойчивости системы (а не колебаний). Применим для систем любого порядка.
Допущения:
- В системе возможны периодические процессы.
- В системе должен быть только один нелинейный элемент.
- Нелинейный элемент должен быть стационарен.
- Линейная часть должна обладать свойством фильтра, т.е. значительно уменьшать амплитуду высших гармоник.
Уравнение системы в параметризованном виде:
Структурная схема:
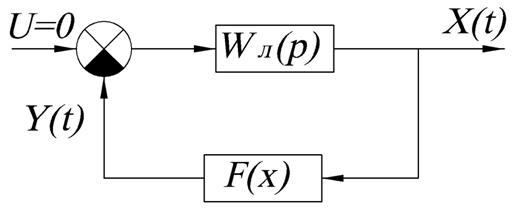
Рисунок 93.
Автоколебания получаются при отсутствии входного воздействия U.
В общем случае
нелинейный элемент может быть статическим или динамическим. Для простоты
рассматриваем статический случай. 
- динамический
элемент, создающий динамическую нелинейность отсутствует.
-операторная
форма записи линейной части
|
Рисунок 94. |
Для
возникновения автоколебаний система должна обладать свойством фильтра,
поэтому степень полинома R(p)
Должна быть выше степени полинома Q(p).
В этом случае при
|
Периодический выходной
сигнал 
можно разложить в ряд Фурье при
входном сигнале 
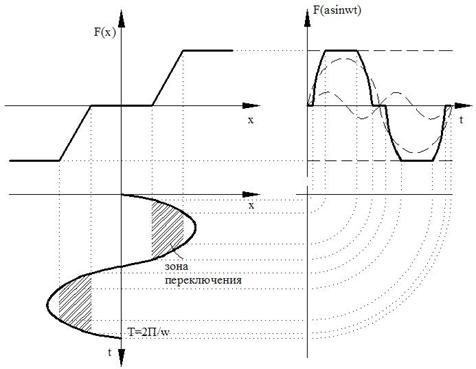
Рисунок 95.
На входе имеем гармонический сигнал, а на выходе получаем сумму гармоник, которая, в результате нелинейности, преобразуется в гармонический сигнал.
Свойства фильтра:
при n=2,3..
Обычно в ряде систем амплитуда высших гармоник значительно меньше чем амплитуда первой. Тогда для первого приближения откидываем все высшие гармоники.
В реальных расчётах сначала делается расчёт по 1-му приближению, и если необходимо, то дальше.
1) Вычисления коэффициентов гармонической линеаризации для симметричных колебаний
- A0=0 (постоянное смещение)
- u=0 (входные воздействия, по условию, равны нулю)
- нелинейность по форме должна быть симметрична
-
Входной сигнал должен быть симметричен (
)
Подставляем в уравнение гармонического разложения
где q, q’- коэффициенты гармонической линеаризации
Введём Ψ=ωt.
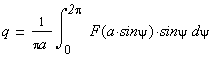
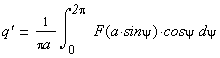
Таким образом, были получены формулы для вычисления коэффициентов нелинейности F(x). Коэффициенты q и q’ называются коэффициентами гармонической линеаризации.
Получим линеаризованную функцию в виде:
-
По Лапласу:
- линеаризованная передаточная
функция
- АЧХ зависит только от амплитуды
-
ФЧХ
Обычно угол φ отрицателен для гистерезисных нелинейностей с запаздыванием
Подставим jω вместо S
Для данного периодического
решения передаточная функция 
линейна при
условии, что амплитуда a постоянна. Нелинейность
заключается в зависимости этой функции от амплитуды входного сигнала a.
АЧХ, зависит от a и не зависит от ω.
При динамической нелинейности в виде F(x, px, p2x, ......) также справедливо разложение в ряд Фурье, при этом коэффициенты гармонической линеаризации q, q’ зависят и от амплитуды a, и от частоты ω. q = q(a, ω), q’= (a, ω).
В соответствии уравнение линеаризованной системы принимает следующий вид:
2) Вычисления коэффициентов гармонической линеаризации для несимметричных колебаний
Причины несимметричных колебаний:
1) Несимметричные входные колебания;
2) смещение.
Решения будем искать в виде: x = x0+ asin(ωt) = x0+x*, где x*= asin(ωt)
Появляется постоянная составляющая F0 (x0, a), коэффициенты q и q’ зависят от смещения
x0
Уравнение системы можно разбить на 2 уравнения: для постоянной составляющей и для гармонического сигнала
3) Вычисление коэффициентов гармонической линеризации для симметричных колебаний
Упрощения: для однозначной нечётной симметричной функции F(x) коэффициент q`=0
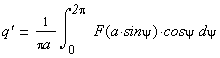
Пример:
|
Рисунок 96. Случай а) |
Рисунок 97. Случай б) |
|
Рисунок 98. Случай в) |
Рисунок 99. Случай г) |
|
Рисунок 100. Случай д) |
|
а) Общий случай.
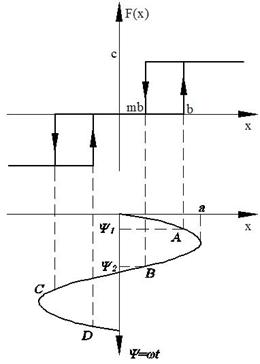
Рисунок 101.
Если
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
- механическая связь
- электрическая связь
- угол поворота
выходного вала редуктора
,
(АЧХ стремится к нулю)
