Лекции по нелинейным системам, страница 7

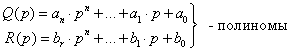
Нормальная форма Коши:

 

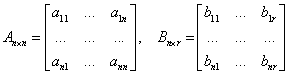
Т.к. входного воздействия нет, то .

Характеристическое уравнение для нормальной формы Коши:

Уравнение 2-го порядка (нормальная форма Коши):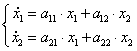

Обычно, для реальной системы справедливо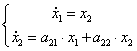

(фазовый вектор – частный случай)

Направление движения по фазовой траектории (для частного случая)

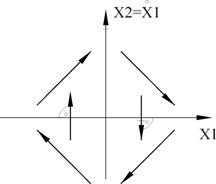
Рисунок 16 – Направление движения по фазовой траектории

 

Для общего случая движение по фазовой траектории может идти в другом направлении.

 

Дифференциальное уравнение фазовой траектории:

Проинтегрировав это уравнение, получим уравнение фазовой траектории

Для построения переходных процессов обычно используются преобразования Лапласа (справедливо только для линейных систем):

Изображение по Лапласу:

Переходный процесс по Лапласу:

- переходный процесс.

Для исследования устойчивости системы используется характеристическое уравнение.

Производим замену :

- характеристический полином.

Для исследования устойчивости системы используются 3 общих критерия: