Лекции по нелинейным системам, страница 5

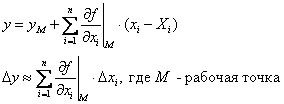
      Частные случаи:

-  Алгебраическая линеаризация: нелинейная функция одной переменной заменяется приближенным выражением.

-  Графическая линеаризация: используется в том случае, если нелинейность задана в графической форме (например, функция намагничивания)

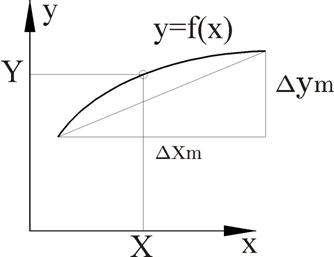
Рисунок 12 – Графическая линеаризация

Метод гармонической линеаризации.

Используется с целью определения автоколебаний, т.е. устойчивых предельных циклов: определить параметры автоколебаний и определить их устойчивость. Используется для исследования устойчивости систем любого порядка.

Допущения метода:

1)  В системе должен быть только один нелинейный элемент (несколько нелинейных элементов сводятся в один). Система разбивается на две части: линейную и нелинейную.

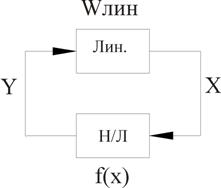
Рисунок 13 – Система с одним нелинейным (Н/Л) элементом

2)  В системе возможны периодические решения, в том числе и автоколебания.

3)  Нелинейный элемент должен быть стационарным.

4)  Линейная часть должна обладать свойством фильтра. При этом должна уменьшаться амплитуда высших гармоник. Обычно, для реальных систем это справедливо.

, на выходе получается практически единая гармоника, т.е. хорошо пропускается только первая гармоника.

Передаточная функция – отношение изображений выходного сигнала по Лапласу ко входному.

Степень многочлена R(S) должна быть меньше, чем Q(S), тогда при (свойство фильтра)

Выходной сигнал y=f(x) можно разложить в ряд Фурье: