Лекции по нелинейным системам, страница 6

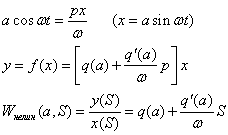
зависит не только от частоты, но и от амплитуды входного сигнала х, т.е. мы произвели замену нелинейного элемента эквивалентным линейным.

 

Метод фазового пространства (пространства состояний)

            Рассматриваются одномерные, стационарные системы 2-го порядка. Метод используется для исследования переходных процессов, определения устойчивости системы и выявления автоколебаний.

            Исходное уравнение нелинейной n-мерной системы:

Таким образом, изучаемая система:

Система 2-го порядка: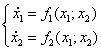

Плоскость называется фазовой плоскостью (для систем 2-го порядка)

- радиус вектор

- фазовая траектория

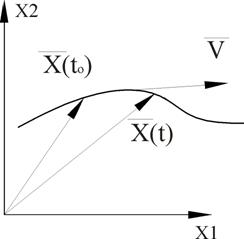
Рисунок 14 – Изображение фазовой траектории на фазовой плоскости

 

Кривая, соединяющая изображающие точки называется фазовой траекторией.

 

Фазовые портреты линейных систем.

Фазовый портрет – совокупность фазовых траекторий при различных начальных условиях. Необходимо показать все типовые фазовые траектории.

Линейные системы

Операторная форма записи:

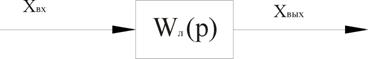
Рисунок 15 – Линейная система