Определение процента годной продукции и требуемой точности настройки раскряжевочной установки

Введение.

Высокие темпы развития теоретических наук на основе хорошо проработанного математического аппарата и необходимостью их экспериментального подтверждения требует из-за медленного развития технологий все более и более дорогостоящих экспериментов. При любом эксперименте невозможно избежать воздействия некоторых неучтенных помех, несмотря на стремление исследователя свести их к минимуму. Большинство из этих воздействий имеет случайную природу. Для возможности их частично компенсировать было разработано целое под направление математики - математическая статистика, которая позволяет оценивать параметры с частичным исключением помех. На получение практических навыков использования данного аппарата направлены задачи 1 и 2.

Задача 1.

Определение процента годной продукции и требуемой точности настройки раскряжевочной установки.

Исходные данные: n - количество наблюдений; l_i - наблюдаемые длины сортиментов после раскряжевки, заданные в виде простого статистического ряда (допустимые отклонения в точности ±1 см на 1 м длины сортимента).

Значения исходных данных для решения задачи приведены в табл. 1.1.

Таблица 1.1.

Исходные данные для определения процента годной продукции и требуемой точности настройки раскряжевочной установки.

1. Заданные в виде простого статистического ряда длины сортиментов необходимо расположить в виде неубывающей последовательности, т.е.

построить вариационный ряд табл.1.2.

Таблица 1.2.

Расположение результатов наблюдений в виде вариационного ряда.

2. С помощью t - критерия Стьюдента исключить из вариационного ряда анормальные результаты наблюдений. Для этого по данной выборке вычисляются:

-    выборочное среднее

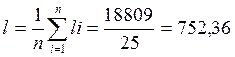см

-    выборочная дисперсия

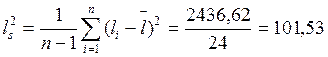
-    выборочное среднеквадратическое отклонение

см

-    расчетный t - критерий

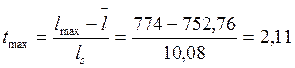
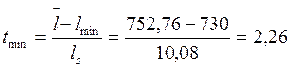
По числу степеней свободы f = n - 1 = 24 и принятому уровню значимости q = 0,05 определяют t - критерий Стьюдента. Если t_max > t и t_min > t, то гипотеза отвергается, значения l_max и l_min признаются анормальными и из выборки исключаются. Проверку такого рода необходимо производить до тех пор, пока не выполнится условие: t_max < t и t_min < t.

2,11 > 2,06 и 2,26 > 2,06