Определение процента годной продукции и требуемой точности настройки раскряжевочной установки, страница 8

t-критерия Стьюдента для заданного уровня значимости q и числа степеней свободы f_в, с которым определялась дисперсия воспроизводимости S_B². Если t_i < t_табл, то коэффициент регрессии b_iнезначим и соответствующий член в уравнении регрессии должен быть отброшен.

Следует иметь в виду, что знак коэффициента регрессии b_i свидетельствует о характере влияния соответствующего фактора. Если b_i < 0, то с ростом X_i отклик уменьшается. Если b_i> 0, то с ростом значений фактора X_i выходная величина растет. Чем больше абсолютная величина линейного коэффициента регрессии в модели, тем сильнее влияние соответствующего фактора.

6. Проверить адекватность модели.

Проверка адекватности математической модели дает возможность экспериментатору ответить на вопрос, будет ли построенная модель предсказывать значения выходной величины с той же точностью, что и результаты эксперимента. Адекватность модели проверяется в следующем порядке:

6.1.  Определяют   сумму   квадратов,   характеризующую   адекватность модели. При неравномерном дублировании ее рассчитывают по формуле:

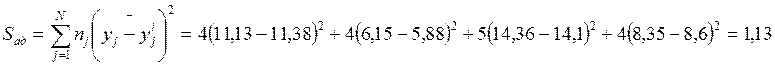
где n_j- число дублированных опытов в j-той серии.

6.2.  Вычисляют число степеней свободы f_ад дисперсии адекватности:

где Р - число коэффициентов в уравнении регрессии.

6.3. Вычисляют дисперсию адекватности S_ад²:

6.4. С помощью F-критерия Фишера проверяют однородность дисперсии адекватности S_ад² и дисперсии воспроизводимости S_в². При этом вычисляют F_расч, которое сравнивают с табличным значением F-критерия , F_табл ,найденное при выбранном уровне значимости q для чисел степеней свободы f_ад в числителе и f_в в знаменателе. Если F_расч < F_табл ,то модель считается адекватной и может быть использована для описания объекта. В противном случае модель неадекватна.

7. Построение графика зависимости П_ч = f(l_тр; V_хл) для нормализованных и натуральных факторов:

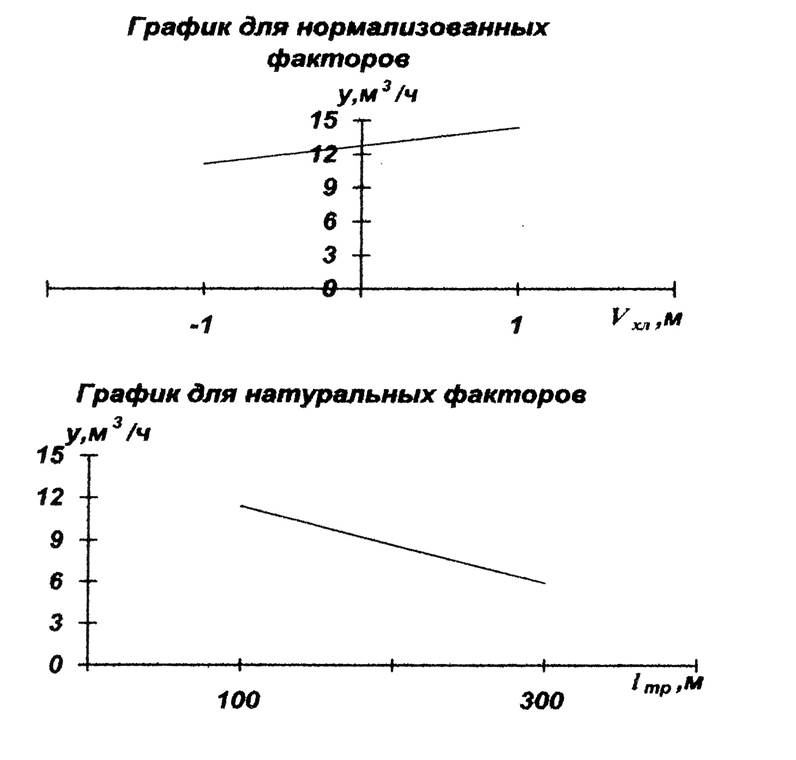
Вывод:   по   результатам   эксперимента   была   получена   следующая регрессионная модель:

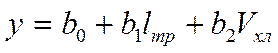
Задача 5.

Оптимальный раскрой хлыста методом линейного программирования.

1. Выбираем длину хлыста и по графику находим его комлевой диаметр.

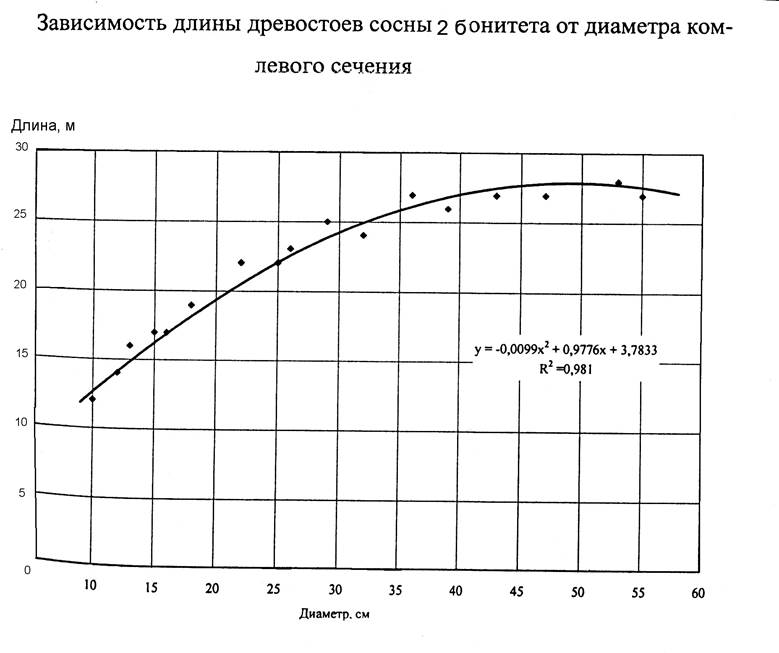
L = 25м.; d_к = 32см.;

Для дальнейших расчётов необходимо использовать средний диаметр хлыста, который находится по формуле:

d_ср = d_к ∙ 0,7

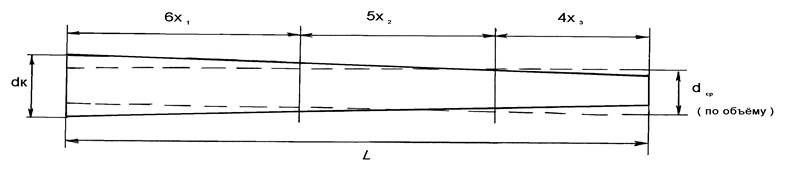
d_ср = 32 ∙ 0,7 = 22,4 см.

2. Исходя из среднего диаметра хлыста d_ср, по графику найдём стоимость одного метра хлыста заданного диаметра.

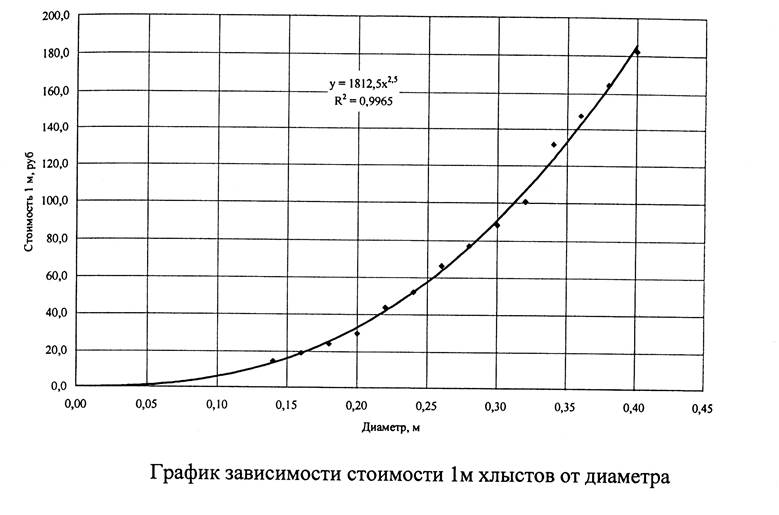
Судя по графику, стоимость одного метра хлыста составит ≈ 45 руб/м.

3. Для определения оптимального раскроя хлыста необходимо построить целочисленные решётки и определить раскрой в узлах, лежащих ближе всего к прямым.

{ 6;5 }; { 6;4 }; { 5;4 }

{ 6;5 }

6x₁ + 5x₂ ≤ 25

Получив целые корни неравенства, построим целочисленную решётку.

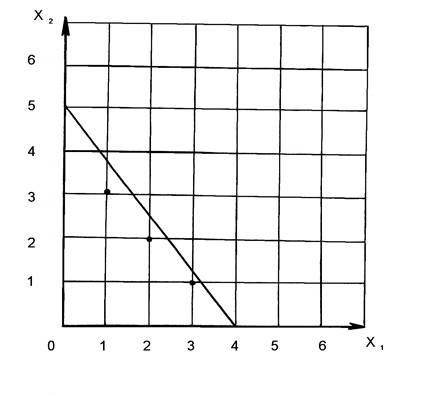
6x₁ + 5x₂ ≤ 25

6∙1 + 5∙3 = 21;

6∙2 + 5∙2 = 22;

6∙3 + 5∙1 = 23;

{ 6;4 }

6x₁ + 4x₃ ≤ 25

Получив целые корни неравенства, построим целочисленную решётку.

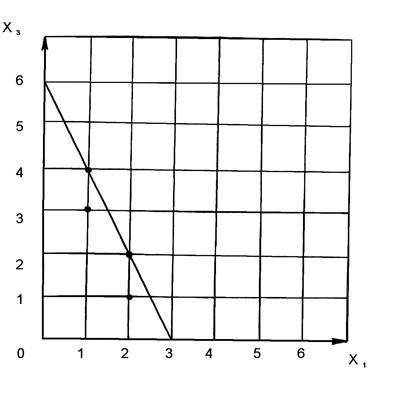
6x₁ + 4x₃ ≤ 25

6∙1 + 4∙4 = 22;

6∙1 + 4∙3 = 18;

6∙2 + 4∙2 = 20;

6∙2 + 4∙1 = 16;

{ 5;4 }

5x₂ + 4x₃ ≤ 25

Получив целые корни неравенства, построим целочисленную решётку.

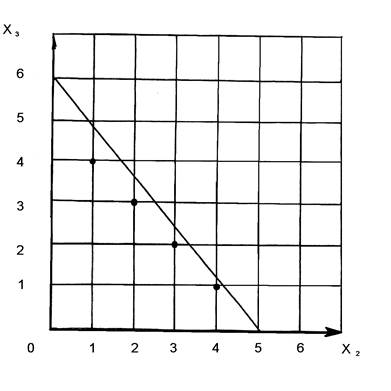
5x₂ + 4x₃ ≤ 25

5∙1 + 4∙4 = 21;

5∙2 + 4∙3 = 22;

6∙3 + 4∙2 = 23;

5∙4 + 4∙1 = 24;

4. Выбираем самый длинный образец и подсчитываем его стоимость, а также отношение раскроенной длины хлыста к нераскроенной:

5∙4 + 4∙1 = 24;

C_p = 24∙45 = 1080 руб;

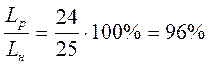   то есть, раскроено 96% хлыста.

Для наглядности представления результатов следует построить пространственную целочисленную решётку:

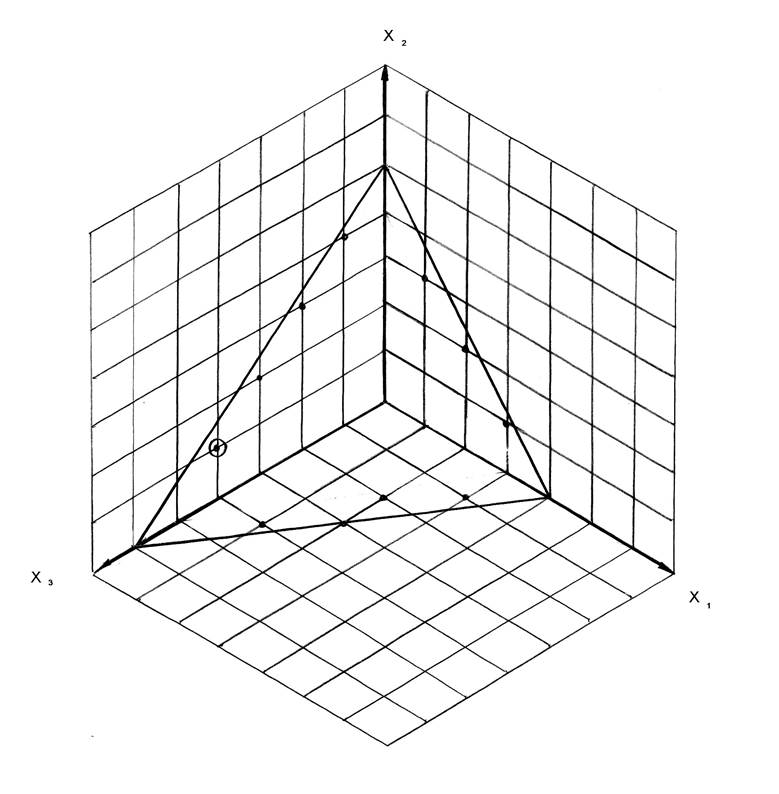
Ответ:

Оптимальный раскрой хлыста: 5∙4 + 4∙1 = 24;

Стоимость раскроя: C_p = 1080 руб;

Отношение раскроенной части хлыста к нераскроенной составляет 96%.

Список использованной литературы.

1. Редькин А.К.   Основы моделирования и оптимизации процессов лесозаготовок. М.: Лесн.  пром-сть, 1988.  256 с.

2.   Пижурин А.А., Розенблит М.С. Основы моделирования и оптимизации процессов деревообработки.  М.: Лесн. пром-сть,  1988.  296 с.                  

3.   Салминен Э.О. Основы моделирования и оптимизации лесотранспорта. Линейное программирование. Текст лекций для студентов специальности 0901: ЛТА. Л., 1987. 52 с.

4.   Тюрин Н.А., Салминен Э.О.  Моделирование и оптимизация процессов лесотранспорта.  Методические указания по выполнению расчетно-графических работ для студентов специальности 26.01: ЛТА. Л,     1990.   37 с.