Определение процента годной продукции и требуемой точности настройки раскряжевочной установки, страница 7

2. Рассчитаем средние (y_i) и дисперсии (S_j²) для каждой серии опытов по формулам:

                                   

                            

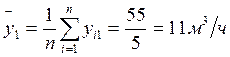
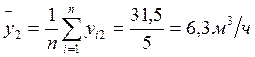
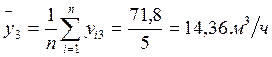
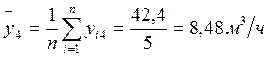
3.     Отбросим   анормальные   результаты   эксперимента.    Проверим однородность дисперсии опытов. Рассчитаем дисперсию воспроизводимости для каждой серии опытов:

                      

                  

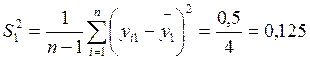
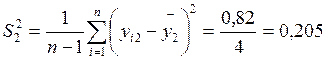
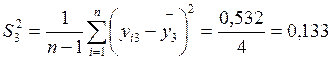
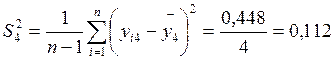
Анормальные результаты эксперимента можно также исключить другим способом. Для этого необходимо найти интервал математического ожидания (M_y) для каждой выборки:

где 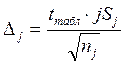 - величина максимальной ошибки j – той серии опытов.

10,56 ≤ M_y1 ≤ 11,44                                            5,737 ≤ M_y2 ≤ 6,863

14,36 – 0,454 ≤ M_y3 ≤ 14,36 + 0,454                    8,48 – 0,416 ≤ M_y4 ≤ 8,48 – 0,416

13,906 ≤ M_y3 ≤ 14,814                                          8,064 ≤ M_y4 ≤ 8,896

10,5; 6,9; 9,0 – являются промахами.

Таблица 4.2.

Факторы				Результаты эксперимента					Результаты расчёта
натуральные		нормализо ванные		y1	y2	y3	y4	y5	yсрi	Sj2	yi*
lтр, м	Vxл,m3	x1	x2
100 300 100 300	0,40 0,40 0,70 0,70	-1  1 -1  1	-1 -1  1  1	5,9 14,7 8,1	10,8 5,8 14,1 8,3	11,1 6,4 14,2 8,5	11,4 6,5 14,8 8,5	11,2   14,0	11,13 6,15 14,36 8,35	0,063 0,123 0,133 0,037	11,38 5,88 14,1 8,6

Для проверки однородности нескольких дисперсий при равных объемах выборок n₁ = n₂ = … = n может быть использован G-критерий Кохрена. Пусть N - количество выборочных дисперсий, однородность которых проверяется. Обозначим эти дисперсии S₁², S₂²... S_n². Вычисляется расчетное G-отношение по формуле:

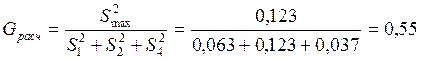
В числителе этой формулы стоит наибольшая из рассматриваемых дисперсий, а в знаменателе - сумма всех дисперсий. По выбранному уровню значимости q, числу степеней свободы каждой выборки f = n – l = 4 и по количеству выборок N из таблиц Кохрена отыскиваем величину

G = G_табл = 0,63

Если G_расч < G_табл , 0,55 < 0,63, то можно принять гипотезу об однородности дисперсий. В противном случае она отвергается.

Проверка однородности дисперсий в выборках по F-критерию Фишера. Для этого вычисляется величина F_paсч, равная отношению большей из выборочных дисперсий к меньшей. Пусть S₂² < S₃² , где S₂ и S₃ - выборочные дисперсии, найденные по выборкам соответственно у₂ и у₃.

Тогда:

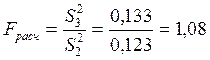
Далее задаемся уровнем значимости q = 0,05 и вычисляем числа степеней свободы дисперсий числителя и знаменателя по формулам:

f₁ = n₁ - 1 = 3  и  f₂ = n₂ - 1 = 4;

где n₁и n₂ - количество измерений соответственно в первой и во второй выборках.

По величинам q, f₁ и f₂ из таблиц распределения Фишера отыскиваем величину F = F_табл = 6,59. Если F_pacч > F_табл, то выборочные дисперсии считаются неоднородными для выбранного уровня значимости. Если

F_pacч < F_табл, 1,08 < 6,59, то можно принять гипотезу об однородности дисперсий.

При различном объеме выборок дисперсия воспроизводимости определяется по формуле:

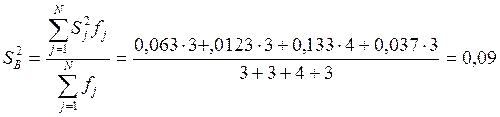
где - число степеней свободы дисперсий.

Число степеней свободы дисперсий воспроизводимости равно:

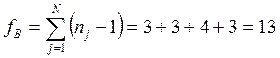
4. Рассчитать коэффициенты регрессионной модели вида y = b₀ + b₁x₁для нормализованных и натуральных факторов. Найти функции отклика.

Коэффициенты регрессии модели рассчитываются по формулам:

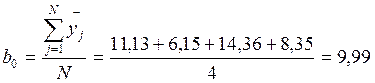
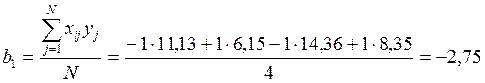
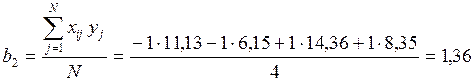
Регрессионная модель в натуральных обозначениях будет иметь вид:

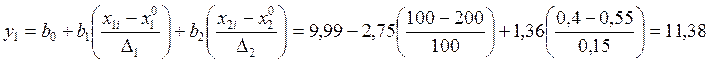
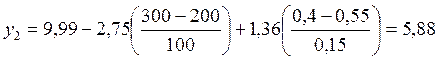
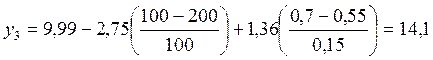
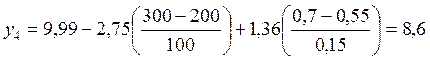
5. Оценить степень значимость коэффициента регрессии.  Для этого используется  t-критерий Стьюдента. Для каждого коэффициента регрессии отыскивается t-отношение:

; t₂= 2,75/0,067 = 41;  t₃= 1,36/0,067 = 20,3

- эмпирический стандарт

где b_i - абсолютная величина коэффициента регрессии.

Вычисленную величину t сравнивают с табличным значением t_табл