Определение процента годной продукции и требуемой точности настройки раскряжевочной установки, страница 5

6. Определяем потребный объем случайной выборки. Если задаться допустимой производственной точностью шероховатости поверхности пиломатериалов Δ и доверительной вероятностью β = l – q = l - 0,05  =  0,95, то можно при данных значениях среднеквадратического отклонения определяем потребный   объем   выборки,   т.е.   необходимое   количество   замеров   (n), гарантирующих данную точность:

               

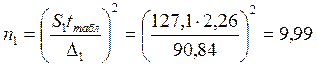
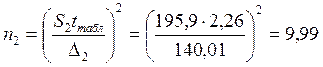
Вывод: анализ статистических свойств результатов измерений шероховатости поверхности пиломатериалов показал, что дисперсии однородны. Потребный объем случайной выборки 10.

Задача 3.

Определение зависимости шероховатости выпиливаемых досок от времени работы рамных пил после заточки рамных пил и шероховатостью поверхности.

Исходные данные: х - время работы пил после заточки, ч; у - шероховатость поверхности досок, мм. Значения исходных данных для решения задачи приведены в табл. 3.1.

Таблица 3.1.

Исходные данные для определения зависимости между временем заточки рамных пил и шероховатостью поверхности выпиливаемых досок.

№ п/п	xi	xi2	xiyi	yi	yi2
1	1	1	0,32	0,32	0,1024
2	2	4	0,74	0,37	0,1369
3	3	9	1,17	0,39	0,1521
4	4	16	1,76	0,44	0,1936
5	5	25	2,50	0,50	0,25
Σ	15	55	6,49	2,02	0,835

1. Определяем коэффициент корреляции (r) между временем работы пил после заточки (t) и шероховатостью поверхности выпиливаемых досок (h).

Коэффициент корреляции характеризует не всякую, а только линейную зависимость между случайными величинами и принимает значения в пределах: -1 ≤ r ≤ 1.

При r > 0 с возрастанием одной из случайных величин другая, в среднем, тоже возрастает, а при r < 0 с возрастанием одной из них другая величина будет в среднем убывать. Чем ближе величина r к (+1) или (-1), тем больше степень линейной зависимости между рассматриваемыми случайными величинами. И, наконец, r = 0 говорит об отсутствии линейной статистической связи между ними (некоррелированные случайные величины).

Обозначим через х - время работы рамных пил после заточки, а.

у - шероховатость поверхности доски.

Коэффициент корреляции вычисляется по формуле:

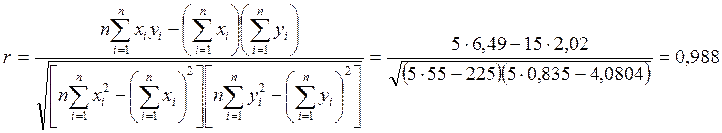
Оценка значимости коэффициент корреляции производится с помощью t-критерия. Для этого определяется:

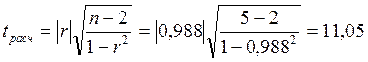
Из таблицы распределения Стьюдента по числу степеней свободы

f = n - 2 = 3 и принятому уровню значимости q = 0,05 находим t_табл = 3,18. Если t_расч < t_табл 3,18 < 11,05, принимаем гипотезу о некоррелированности величин х и у. В противном случае r значимо отличается от 0, т.е. между величинами х и у существует линейная статистическая связь.

2. Оценить коэффициенты регрессии линейной и квадратичной моделей.

В задаче рассматривается случай варьирования единственного фактора X - величины работы рамных пил после заточки. Обозначим через Y выходную величину - шероховатость поверхности доски.

Регрессионная модель в виде линейного уравнения имеет вид:

у = ах + b

Коэффициенты регрессии можно определить, решив систему из двух линейных уравнений с двумя неизвестными:

     

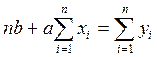
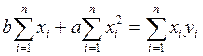
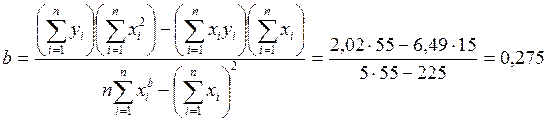
Решая ее, придем к искомым формулам.

По полученной зависимости необходимо вычислить значения отклонения y_i* и сравнить с экспериментальными. Построить график зависимости h* = f(t).

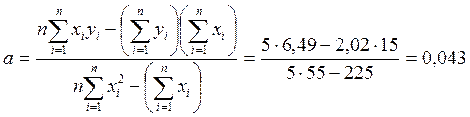
y₁* = 0,043 ∙ 1 + 0,275 = 0,318

у₂* =  0,043 ∙ 2 + 0,275 = 0,361

y₃* = 0,043 ∙ 3 + 0,275 = 0,404

y₄* = 0,043 ∙ 4 + 0,275 = 0,447

y₅* = 0,043 ∙ 5 + 0,275 = 0,49

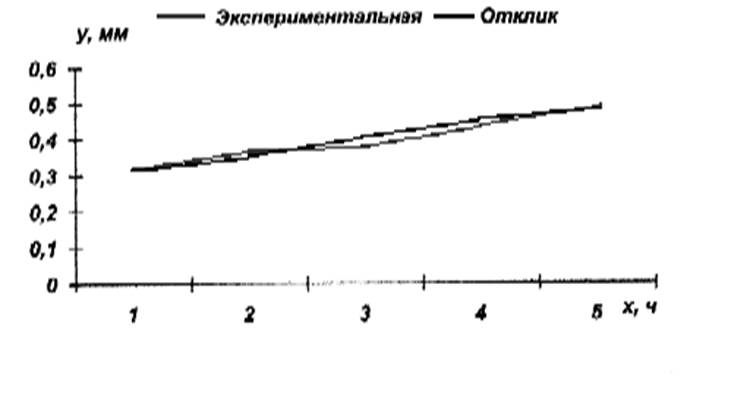
Регрессионная модель в виде квадратичного уравнения имеет вид:

у = ах² + bх + с

Для отыскания трех неизвестных коэффициентов регрессии а, b и c надо решать следующую систему из трех линейных уравнений с тремя неизвестными:

a_2xa + a_1xb + a_0xc = a₀₁xy

a_3xa + a_2xb + a_1xc = a₁₁xy

a_4xa + a_3xb + a_2xc = a₂₁xy

   

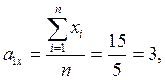
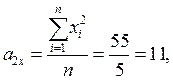
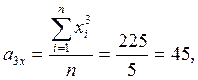
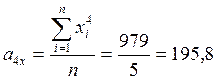
11a + 3b + 0,2c = 0,4