Определение процента годной продукции и требуемой точности настройки раскряжевочной установки, страница 3

С помощью t - критерия Стьюдента исключить из вариационного ряда анормальные результаты наблюдений. Для этого по данной выборке вычисляются:

-    выборочное среднее

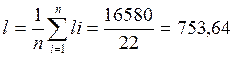см

-    выборочная дисперсия

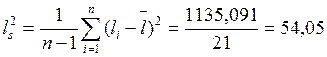
-    выборочное среднеквадратическое отклонение

см

-    расчетный t - критерий

                      

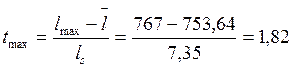
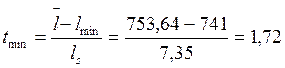
По числу степеней свободы f = n - 1 = 21 и принятому уровню значимости q = 0,05 определяют t - критерий Стьюдента. Если t_max > t и t_min > t, то гипотеза отвергается, значения l_max и l_min признаются анормальными и из выборки исключаются. Проверку такого рода необходимо производить до тех пор, пока не выполнится условие: t_max < t и t_min < t.

1,82 < 2,08 и 1,72 < 2,08

Условие выполнено.

4. Построение гистограммы начинается с определения числа разрядов, т.е. интервалов, для которых в дальнейшем вычисляют относительные или абсолютные частоты, т.е. количество попаданий той или иной случайной величины в интервал.

Число интервалов может быть определено по формуле:

k = 1 + 3,2 lg n = 1 + 3,2 lg 22 = 5

Шаг интервала может выбираться произвольно или по формуле

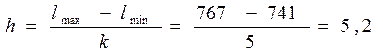
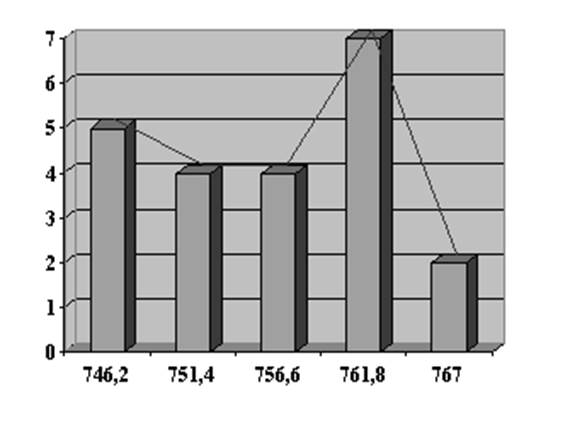
Полученные данные удобно свести в табл. 1.5.

Таблица 1.5.

Данные для построения гистограммы и проверки степени согласования экспериментальных и теоретических законов

Номер интервала	1	2	3	4	5
Границы интервала	741-746,2	746,2-751,4	751,4-756,6	756,6-761,8	761,8-767
Середина интервала	743,6	748,8	754	759,2	764,4
Экспериментальная частота, me	5	4	4	7	2
Теоретическая частота, n * meT	2,7347	4,278	5,842	4,991	2,8382

В соответствии с полученными данными строится гистограмма, которая может иметь вид:

5. Задаться теоретическим законом распределения случайной величины (размеры сортимента) и определить значения теоретических частот (n * m_e^T для каждого интервала).

Возьмем нормальный закон распределения:

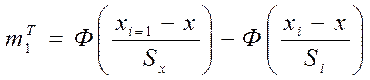
где Ф (...)- интегральная функция распределения; x- выборочное среднее;

S_x -выборочное среднеквадратическое отклонение.

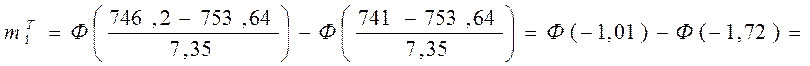= (1-0,841) - (1-0,9554) = 0,159 - 0,0446 = 0,1144

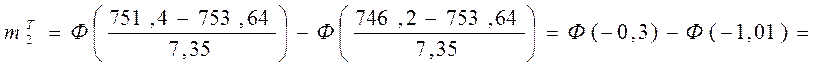= (1-0,618) - (1-0,841) = 0,382 - 0,159 = 0,223

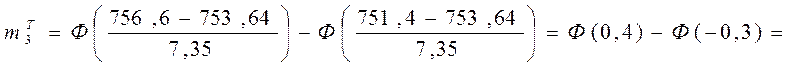= 0,655 - (1-0,618) = 0,327

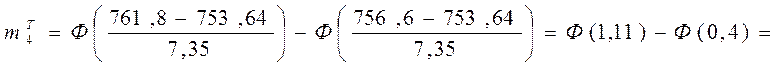= 0,864 – 0,655 = 0,209

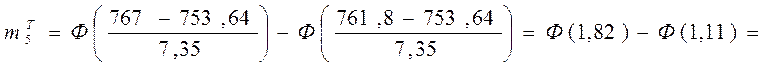= 0,9641 – 0,864 = 0,1001

6. Проверка согласования по критерию Пирсона имеет следующий вид:

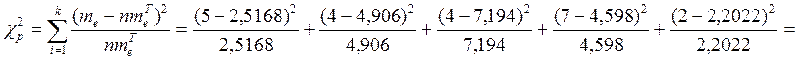
= 2,45 + 0,1673 + 1,4181 + 1,2548 + 0,0186 = 5,3088

По числу степеней свободы F = k-3= 2 и заданном уровне значимости q определяем значение χ²_табл. Если χ_р² < χ²_табл , то гипотеза о соответствии теоретического закона распределения экспериментальному принимается. В противном случае необходимо выбрать другой закон распределения. χ²_табл  = 5,99

5,3088 < 5,99

Вероятность  попадания  случайной  величины  (длины сортимента)  в заданный интервал для нормального закона определяется по формуле:

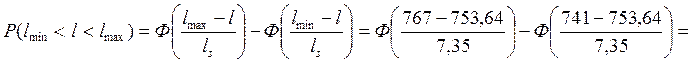
= Ф(1,82) - Ф(-1,72) = 0,9641 - (1 - 0,9554) = 0,9195

Выход готовой продукции 91,95 %.

Вывод: случайная величина распределяется по нормальному закону распределения. При хорошо налаженной установке выход готовой продукции должен быть не меньше 92 %.

Задача 2.

Анализ статистических свойств результатов измерений шероховатости

поверхности пиломатериалов.

Исходные данные: результаты наблюдений шероховатости поверхности пиломатериалов в виде двух выборок у₁ и у₂..Значения исходных данных для решения задачи приведены в табл.2.1.

Таблица 2.1.

Исходные данные для анализа статистических свойств результатов измерений шероховатости поверхности пиломатериалов.

y1, высоты микронеровностей на поверхности доски, мкм	680	850	840	840	940	990	550	850	860	900
y2,высоты микронеровностей на поверхности доски, мкм	454	940	685	910	850	910	550	560	430	660