Определение процента годной продукции и требуемой точности настройки раскряжевочной установки, страница 4

1. Расположение результатов наблюдений в виде вариационного ряда представлена в табл. 2.2.

Таблица 2.2.

Расположение результатов наблюдений в виде вариационного ряда.

Выборка	y1	y1i-yср	(y1i-yср)2	y2	y2i-yср	(y2i-yср)2
1	680	-150	22500	454	-240,9	58032,81
2	850	20	400	940	245,1	60074,01
4	840	10	100	685	-9,9	98,01
3	840	10	100	910	215,1	46268,01
5	940	110	12100	850	155,1	24056,01
6	990	160	25600	910	215,1	46268,01
7	550	-280	78400	550	-144,9	20996,01
8	850	20	400	560	-134,9	18198,01
9	860	30	900	430	-264,9	70172,01
10	900	70	4900	660	-34,9	1218,01
Σ	8300		145400	6949		345380,9

2. С помощью t - критерия Стьюдента исключить из вариационного ряда анормальные результаты наблюдений. Для этого по данной выборке вычисляются:

-    выборочное среднее

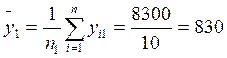мкм

-    выборочная дисперсия

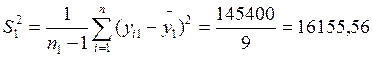
-    выборочное среднеквадратическое отклонение

мкм

-    расчетный t - критерий

                      

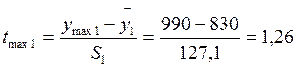
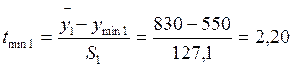
-    выборочное среднее

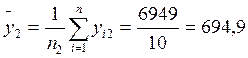мкм

-    выборочная дисперсия

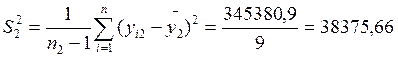
-    выборочное среднеквадратическое отклонение

мкм

-    расчетный t - критерий

                      

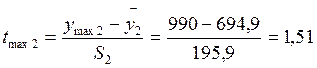
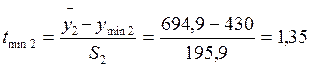
По числу степеней свободы f = n - 1 = 9 и принятому уровню значимости q=0,05 определяют t - критерий Стьюдента, t = 2,26. Если t_tnax > t и t_min > t, то гипотеза отвергается, значение y_mах и y_min признаются анормальными и из выборки исключаются. Проверку такого рода необходимо производить до тех пор, пока не выполнится условие: t_tnax < t и t_min < t; 1,26 < 2,26 и 2,2 < 2,26; 1,51 < 2,26 и 1,35 < 2,26.

Условие выполнено.

3. Проверка однородности дисперсий в выборках по F-критерию Фишера. Для этого вычисляется величина F_paсч, равная отношению большей из выборочных дисперсий к меньшей. Пусть S₁² < S₂², где S₁² и S₂² – выборочные дисперсии, найденные по выборкам соответственно y₁и > y₂. Тогда:

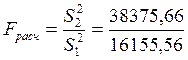 = 2,38

Далее задаемся уровнем значимости q = 0,05 и вычисляем числа степеней свободы дисперсий числителя и знаменателя по формулам:

f₁ = n₁ – 1 = 9 и f2 = n₂ – 1 = 9

где n₁ и n₂ - количество измерений соответственно в первой и во второй выборках. По величинам q, f₁ и f₂ из таблиц распределения Фишера отыскиваем величину F = F_табл = 3,18. Если F_paсч > F_табл, то выборочные дисперсии считаются неоднородными для выбранного уровня значимости. Если F_paсч < F_табл, 2,38 < 3,18, то можно принять гипотезу об однородности дисперсий.

4. Проверка однородности выборочных средних.

Дисперсии S₁² и S₂² однородны. Вычисляем расчетный t-критерий Стьюдента по формуле:

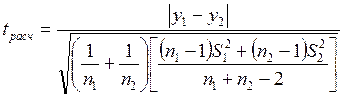
где y₁ и y₂ - средние соответственно первой и второй выборок.

Если обе выборки имеют одинаковый объем, т.е. n₁ = n₂ = n, то формула упрощается:

5. Оцениваем точность и надежность оценки математического ожидания.

Доверительный интервал для математического ожидания равен:

y – Δ ≤ M_y ≤ y + Δ

где Δ - величина максимальной ошибки.

Максимальные ошибки для выборок определяются по формуле:

             

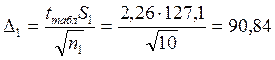
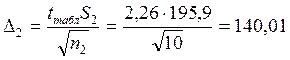
Значение t_таблвыбирается из таблицы распределения Стьюдента по числу степеней свободы (f₁ = n₁ – 1 = 9 и f₂ = n₂ - 1 = 9) и принятому уровню значимости q.

y₁ – Δ₁ ≤ M_y ≤ y₁ + Δ₁

830 – 90,84 ≤ M_y ≤ 830 + 90,84

739,16 ≤ M_y ≤ 920,84

y₂ – Δ₂ ≤ M_y ≤ y₂ + Δ₂

694,9 – 140,01 ≤ M_y ≤ 694,9 + 140,01

554,89 ≤ M_y ≤ 834,91