Исследование статики объекта методом активного эксперимента. Описание статической характеристики объекта с одной входной и одной выходной величинами линейным уравнением

3. ЭКСПЕРИМЕНТАЛЬНЫЙ МЕТОД ПОСТРОЕНИЯ МАТЕМАТИЧЕСКОЙ МОДЕЛИ.

В экспериментальном методе принимаются три допущения:

1.  объект рассматривается с сосредоточенными параметрами;

2.  статические и динамические свойства объекта не изменяются во времени;

3.  уравнения статики и динамики можно линеаризовать в малом в окрестности установившегося состояния.

Различают активный и пассивный экспериментальные методы построения математической модели. В первом методе значения и характер входных величин устанавливают экспериментаторы. Во втором методе используется случайные изменения входных параметров в процессе нормальной эксплуатации объекта.

3.1. Исследование статики объекта методом активного эксперимента

Процесс построения экспериментальной модели активным экспериментальным методом включает в себя три основных этапа:

1.  подготовку и планирование эксперимента,

2.  проведение эксперимента,

3.  обработку результатов.

На первом этапе изучается технологический режим работы объекта, выявляются возмущения воздействия, управляющие воздействия, выходные регулируемые и контролируемые величины, допустимые диапазоны изменения режимных параметров объекта. Составляется априорная структурная схема объекта. Затем производятся разделение общей структурной схемы объекта на элементарные схемы с одним входом и одним выходом. Следует заметить, что при наличии у объекта нескольких входов и выходов, внутренних прямых и перекрестных связей между ними всегда имеется возможность преобразовать его структурную схему к схеме с несколькими входами и одним выходом.

3.1.1.Описание статической характеристики объекта с одной входной и одной выходной величинами линейным уравнением.

Предварительно оценивается время установления процесса  как время, за которое переходная функция исследуемого объекта достигает 95% своего установившегося значения. Весь диапазон изменения входной переменной  разбивается на  отрезков величиной , т.е.

.                                                                                       

 выбирается таким, чтобы . Время эксперимента оценивается величиной

,                                                                                           где  - длительность наблюдения, которая выбирается из условия

.                                   

В процессе эксперимента дается приращение  входной переменной через промежуток времени и производится измерение выходной величины . По окончании эксперимента получают таблицу соответствий между  и  (), представляющую статическую характеристику .

Наиболее распространенной линейной формой статической характеристики является ее представление линейной частью разложения функции в окрестности рабочего режима

.                                                                  

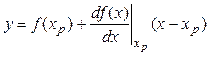Тогда можно записать

,                                                                                      (3.1)

где .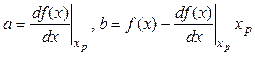   

Если погрешность аппроксимации задана, например , равная ошибке измерения величины , то можно вычислить границы интервала линейности величины  и  входной величины для нелинейной функции  

.                                                  

Если границы линейности ,  и погрешность моделирования заданы, то коэффициенты линейного уравнения (3.1) можно вычислить из системы уравнений

, ,                                           где  и  – экспериментальные значения выходной величины при значениях входной величины соответственно  и .

Если погрешность моделирования не задана, то коэффициенты  и  вычисляются с помощью метода наименьших квадратов. При этом формируется функция отклонения экспериментальных  и расчетных по уравнению (3.1) значений в виде

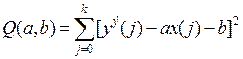.                                                          (3.2)

Коэффициенты a и b определяют из необходимого условия минимума функции (3.2)

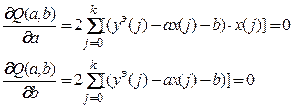.                (3.3)

Доказано, что функция (3.2) унимодальная и имеет минимум. Преобразуем систему уравнений (3.3) к виду:

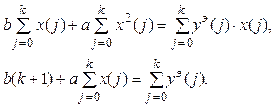                              (3.4)

Решив систему уравнений (3.4), получим  и . Максимальная ошибка моделирования в этом случае определяется как

.                                                    

3.1.2. Описание статической характеристики объекта с одной входной и одной выходной величинами нелинейным уравнением.

Для нелинейного представления статической характеристики используется выражение

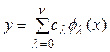,                                               (3.5)

где  - известные функции,  - коэффициенты.

Широкое распространение получили функции  вида , . Если равно числу опытов , то все коэффициенты в выражении (3.5) определяются решением системы линейных уравнений

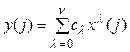, .                                                 (3.6)

В случае  для определения можно воспользоваться методом наименьших квадратов путем минимизации функции

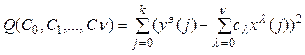.                            (3.7)

Необходимое условие минимума функции (3.7)

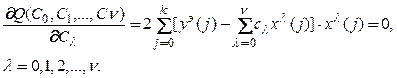      (3.8)

Запишем систему уравнений (3.8) в развернутом виде:

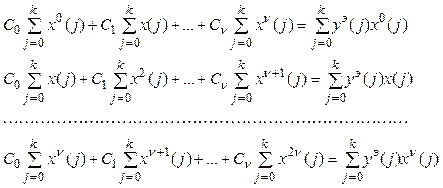(3.9)

Матричная форма системы (3.9)

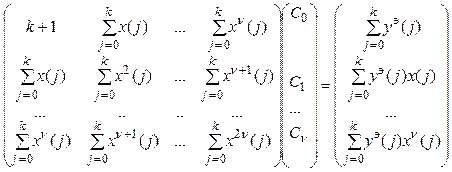, (3.10))

или, введя обозначения ,,, соответствующие содержанию скобок слева направо в выражении (3.10), получим: