Исследование статики объекта методом активного эксперимента. Описание статической характеристики объекта с одной входной и одной выходной величинами линейным уравнением, страница 5

План полного факторного эксперимента с количеством опытов, лежащим между числом опытов полного факторного эксперимента для четырех факторов (16 опытов) и числом искомых коэффициентов (5 коэффициентов) есть план для трех факторов. Этот план дает  опытов. Ниже приведена матрица планирования для трех факторов с учетом взаимодействия.

№ опыта
1	+1	+1	+1	+1	+1	+1	+1	+1
2	+1	+1	-1	+1	-1	-1	+1	-1
3	+1	-1	-1	+1	+1	-1	-1	+1
4	+1	-1	+1	+1	-1	+1	-1	-1
5	+1	+1	+1	-1	+1	-1	-1	-1
6	+1	+1	-1	-1	-1	+1	-1	+1
7	+1	-1	-1	-1	+1	+1	+1	-1
8	+1	-1	+1	-1	-1	-1	+1	+1

Если требуется получить линейное уравнение для четырех факторов, то можно воспользоваться ниже приведённой дробной репликой полученной из рассмотренного выше плана.

№ опыта
1	+1	+1	+1	+1	+1
2	+1	+1	-1	+1	-1
3	+1	-1	-1	+1	+1
4	+1	-1	+1	+1	-1
5	+1	+1	+1	-1	-1
6	+1	+1	-1	-1	+1
7	+1	-1	-1	-1	-1
8	+1	-1	+1	-1	+1

Число опытов, в соответствии с этим планом, составляет половину от числа опытов по плану полного факторного эксперимента для четырех факторов. Эта матрица обозначается  и носит название полуреплики.

Если ввести пятый фактор и приравнять его двойному взаимодействию, например, , то дробность реплики будет , если, то , если , то . Таким образом, введение и использование дробных реплик позволяет сократить общее количество опытов. Переход в полученном уравнении регрессии к натуральным переменным осуществляется раскодированием переменных.

Уравнения поверхности регрессии для  факторов имеет (в закодированных переменных) вид:

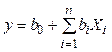                                                              (3.14)

Расчет коэффициентов уравнения(3.14) выполняется по формуле

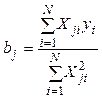,                                                                (3.15)

где  - номер опыта;  - номер коэффициента.

При формировании дробных реплик через эффекты взаимодействия, например , значения в столбце  получает перемножением соответствующих значений  и , а расчет коэффициента  выполняется так же, как и остальных коэффициентов в (3.15), т.е.

.                                                                       

3.1.3.2. Оценка значимости коэффициентов

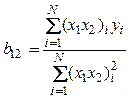Оценку значимости коэффициентов  выполняют по - критерию Стьюдента