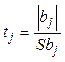Исследование статики объекта методом активного эксперимента. Описание статической характеристики объекта с одной входной и одной выходной величинами линейным уравнением, страница 6

,                                                                         (3.16)

где

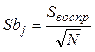,                                                                                в которых  - -ый коэффициент в уравнении регрессии (3.14),  - оценка среднеквадратического отклонения воспроизводимости.

Для расчета  необходимо дополнительно к плану полного факторного эксперимента  поставить серию из  параллельных опытов по любой строке плана. Обычно серию параллельных опытов ставят в нулевой точке, т.е. . В результате этих опытов получают систему значений , ,…, . Тогда

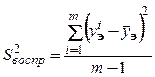,                                                                 где  - значение  в серии параллельных опытов,  - среднее значение  из той же серии

.                                                                                 

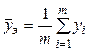Рассчитанное по формуле(3.16) значение - критерия сравнивается с табличным значением при заданных значениях уровня значимости  (или ) и числом степеней свободы (), т.е. . Если

,                                                        то соответствующий коэффициент уравнения регрессии считается незначимым.

Отсутствие корреляции между факторами приводим к тому, что если один из коэффициентов  незначим, то соответствующий член уравнения  исключается, причем остальные коэффициенты пересчитывать не следует.

3.1.3.3. Оценки адекватности уравнения

После оценки значимости коэффициентов уравнения регрессии выполняется процедура оценки его адекватности. Оценка адекватности позволяет сравнить погрешность эксперимента с погрешностью расчета по уравнению регрессии. Оценка адекватности выполняется по - критерию (критерию Фишера)

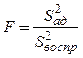,                                                                    (3.17)

где  - оценка дисперсии адекватности

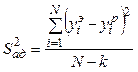,                                                                      где  - значение , полученное в условиях -го опыта (по плану),  - значение , рассчитанное по уравнению регрессии для условий -го опыта,  - число опытов,  - число коэффициентов уравнения регрессии после исключения незначимых коэффициентов.

Рассчитанное значение  сравнивается с табличным для заданного уравнения значимости  по критерию Фишера. Если имеет место

,                                                            (3.17)

то уравнения считаются адекватными.

3.1.4. Экспериментальный метод построения математической модели динамики объекта

Суть метода заключается во внесении искусственного возмущения по одному входному параметру  и в регистрации изменений выходного параметра . Так как экспериментальное исследование динамики объекта проводится по каждому из имеющихся каналов при стабилизированных значениях остальных входных воздействий, то общая структурная схема может быть преобразована в схему объекта с одним входом  и одним выходом . Планирование эксперимента сводится к выбору вида возмущающего воздействия, количества опытов и величины амплитуды испытываемого сигнала.

Испытательные воздействия делятся на апериодические и периодические. К первым относятся следующие сигналы: ступенчатая функция,  прямоугольный импульс. Эти воздействия применяют для снятия переходных функций с промышленных объектов. Периодические испытательные воздействия типа синусоиды и прямоугольной волны применяются для снятия амплитудно-фазовых характеристик объекта. Перед началом динамического пробега устанавливается рабочий режим, стабилизируется работа основных источников возмущений и проверяется правильность работы регистрирующих приборов. При снятии переходных функций испытательный сигнал наносится вручную или с помощью резкого изменения регулирующего органа исполнительного механизма.

Регистрацию изменений выходного параметра  прекращают после того, как система придет в новое установившееся состояние. Полученную кривую разгона обрабатывают, т.е. выделяют время «чистого» запаздывания  и определяют коэффициент усиления .

Далее переходная функция аппроксимируется решением дифференциального уравнения с заранее заданной структурой. За математическую модель динамики исследуемого объекта принимается дифференциальное уравнение, решение которого наиболее близко описывает переходный процесс.