Исследование статики объекта методом активного эксперимента. Описание статической характеристики объекта с одной входной и одной выходной величинами линейным уравнением, страница 2

                                                                                                   (3.11)

Умножим слева обе части равенства (3.11) на матрицу :

.                                                                              

Учитывая, что  – единичная матрица, имеем

.                                                                                    

Порядок  полинома (3.6) для гладких функций , воспроизводимых экспериментально, можно выбрать из условия:

.                                                                               

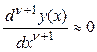С этой целью из экспериментальных данных вычисляют

                         

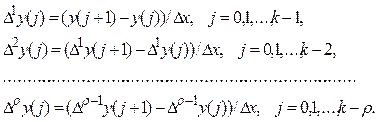
Если при каком-то  выполняется условие

,                                                                      то

.                                                                                       

Если  измеряется с известной погрешностью в виде среднеквадратичной ошибки , то порядок полинома (5.6) может быть вычислен из условия:

.                                   

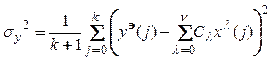В реальных условиях проведения эксперимента выходная величина  измеряется с некоторой погрешностью : , где  – случайный стационарный процесс с нулевым среднем значением. При подготовке и планировании эксперимента в этом случае, как и ранее, устанавливается диапазон изменения входной величины  и определяется . Производится оценка дисперсии  при фиксированном значении . Шаг варьирования (изменения)  выбирается из условия, чтобы при этом шаге изменение выходной величины составило

.                                                                          

В процессе эксперимента при изменении  на величину  на отрезках ) производится измерений  и определяется его среднее значение

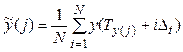.                                                          где .

Если усредненные значения  искажены помехами, то используют сглаживание статической характеристики. Для сглаживания используются несколько методов. Рассмотрим широко распространенный метод сглаживания скользящим средним. При сглаживании этим методом выбирается интервал осреднения (память фильтра) , где  – четное число, и вычисляется среднее от первых  значений :

.                                                              

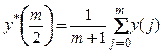Затем интервал осреднения сдвигают на  и вновь вычисляют среднее значение  для интервала , т.е.

.                                                        

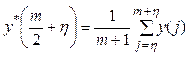При выборе интервала усреднения нужно учитывать, что увеличение  ведет к искажению истинной характеристики, а при малом интервале усреднения слабее усредняется помеха .

3.1.3. Описание статического состояния объекта с одной выходной и несколькими входными переменными. Метод планирования эксперимента

Идея метода планирования эксперимента состоит в проведении опытов при минимальном их количестве для получения уравнения регрессии.

К фактору относится та переменная, для которой имеется способ установить любое ее возможное значение. Факторное пространство - пространство с заданной системой координат, на каждой из осей которой откладывается значение того или другого фактора. К совокупности факторов предъявляется следующие основные требования:

·  отсутствие линейной коррекции между каждой парой факторов,

·  их совместимость.

Требование отсутствия линейной корреляции обусловлено тем, что при включении в эксперимент коррелированных факторов один из них не несет никакой информации.

Несовместимость факторов возникает в том случае, когда невозможно реализовать какую-либо их комбинацию, но при этом значение каждого фактора лежит в допустимых пределах. В общем случае при рассмотрении любого процесса число факторов может быть очень большим. Поэтому при выборе факторов следует попытаться априорно (до опыта) оценить степень их влияния на изучаемую выходную переменную.