Выше были рассмотрены элементарные
расчеты реакторов в применении к простым реакциям, причем особое внимание
уделялось зависимости степени превращения от времени реакции или объема
реактора. В случае более сложных реакции, таких, как параллельные и консекутивные,
получается несколько продуктов; некоторые из них могут быть целевыми ![]() , другие - побочными
, другие - побочными ![]() . Естественно, что в результате
процесса должна быть достигнута не только максимально возможная степень
превращения, но и высокая селективность.
. Естественно, что в результате
процесса должна быть достигнута не только максимально возможная степень
превращения, но и высокая селективность.
Селективность ![]() -
отношение количества полученного целевого продукта
-
отношение количества полученного целевого продукта ![]() к
количеству основного превращенного реагента
к
количеству основного превращенного реагента ![]() .
Когда эти количества выражаются в мольных единицах и учитывается стехиометрия
уравнения реакции,
.
Когда эти количества выражаются в мольных единицах и учитывается стехиометрия
уравнения реакции, ![]() меняется от
меняется от ![]() до
до ![]() .
На основании данного определения
.
На основании данного определения ![]() выражается
уравнением:
выражается
уравнением:
![]() . (7.38)
. (7.38)
Часто для оценки сложного реакционного
процесса используют отношение количеств полученного целевого продукта и
загруженного основного реагента. Это отношение называется выходом продукта ![]() . Легко установить, что
. Легко установить, что
![]() . (7.39)
. (7.39)
Значение ![]() также
меняется от
также
меняется от ![]() до
до ![]() ; оно велико, если селективность и относительная степень превращения
высоки, и наоборот. Выражения (7.38), (7.39) в равной степени относятся как к
простым реакционным системам, так и к кубовым реакторам полунепрерывного
действия и реакторам с поперечным потоком, если
; оно велико, если селективность и относительная степень превращения
высоки, и наоборот. Выражения (7.38), (7.39) в равной степени относятся как к
простым реакционным системам, так и к кубовым реакторам полунепрерывного
действия и реакторам с поперечным потоком, если ![]() и
и
![]() характеризуют реактор в целом.
характеризуют реактор в целом.
Мы будем в основном рассматривать параллельные и консекутивные реакции, в которых распределение продуктов между целевыми и побочными существенно различно.
Это отчетливо видно из рис. 7.5. Так,
в случае параллельных реакций (рис. 7.5а) и ![]() и
и
![]() образуются при любых величинах
образуются при любых величинах ![]() в интервале от
в интервале от ![]() до
до ![]() . Выход
. Выход ![]() (на рис. 7.5 характеризуется
величиной
(на рис. 7.5 характеризуется
величиной ![]() ) возрастает с увеличением степени
превращения.
) возрастает с увеличением степени
превращения.
а б
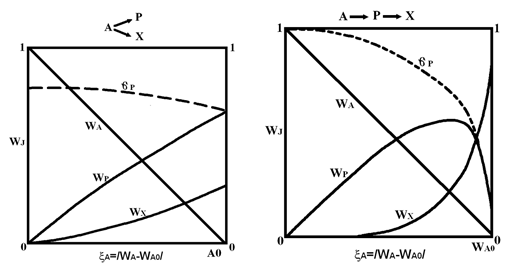 Рис. 7.5. Зависимость концентраций компонентов смеси
и
селективности от степени превращения для параллельной
и консекутивной реакций.
Рис. 7.5. Зависимость концентраций компонентов смеси
и
селективности от степени превращения для параллельной
и консекутивной реакций.
При консекутивных реакциях сначала
образуется ![]() , который затем превращается в
, который затем превращается в ![]() . Поэтому вначале
. Поэтому вначале ![]() , а по мере приближения реакции к
концу эта величина уменьшается до
, а по мере приближения реакции к
концу эта величина уменьшается до ![]() . Следовательно, с изменением степени превращения выход
. Следовательно, с изменением степени превращения выход ![]() проходит через максимум.
проходит через максимум.
Форма кривых на диаграмме, приведенной на рис. 7.5, зависит не только от типа сложной реакции, но и от констант скорости (которые могут заметно меняться с температурой) и от типа реактора. Это продемонстрировано для системы параллельных реакций.
На рис. 7.6 приведена зависимость
величин ![]() и
и ![]() от
относительной степени превращения
от
относительной степени превращения ![]() для реактора
периодического действия, кубового реактора непрерывного действия и
идеализированного реактора с поперечным потоком. Так как компонент
для реактора
периодического действия, кубового реактора непрерывного действия и
идеализированного реактора с поперечным потоком. Так как компонент ![]() может быть превращен только в
целевой продукт
может быть превращен только в
целевой продукт ![]() , из уравнения (7.38)
получаем
, из уравнения (7.38)
получаем ![]() и из (7.39)
и из (7.39) ![]() .
.
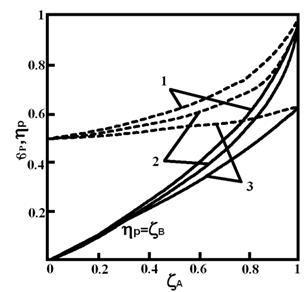 Рис. 7.6.
Селективность и выход для параллельных реакций:
1 - реактор с поперечным
потоком;
2 - кубовый реактор; 3 - реактор периодического действия
Рис. 7.6.
Селективность и выход для параллельных реакций:
1 - реактор с поперечным
потоком;
2 - кубовый реактор; 3 - реактор периодического действия
В трубчатых гомогенных реакторах скорость потока, как правило, весьма велика и гидродинамические условия соответствуют области развитой турбулентности. Можно принять, что для этих условий характерен так называемый режим идеального вытеснения, или поршневой режим, который заключается в следующем:
линейная скорость, концентрации и температура постоянны в пределах каждого поперечного сечения (одноосная модель);
перенос вещества и тепла происходит только в результате гидродинамического движения, а перенос за счет турбулентной диффузии и тем более молекулярной диффузии и теплопроводности пренебрежимо мал и может не учитываться.
Перейдем к математическому описанию
гомогенных реакторов идеального вытеснения. Материальный баланс бесконечно
малого элемента реактора с объемом ![]() по
по ![]() -му компоненту заключается
в том, что отношение приращения потока
-му компоненту заключается
в том, что отношение приращения потока ![]() -го компонента к объему элемента равно скорости образования
-го компонента к объему элемента равно скорости образования ![]() -го компонента, т.е.
-го компонента, т.е.
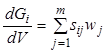 , (7.40)
, (7.40)
где ![]() -
скорость
-
скорость ![]() -ой реакции, определяемая как
-ой реакции, определяемая как ![]()
![]() .
.
Поток ![]() -го компонента выражается через концентрации следующим образом:
-го компонента выражается через концентрации следующим образом:
![]() (7.41)
(7.41)
где ![]() -
массовый поток реакционной смеси,
-
массовый поток реакционной смеси, ![]() ;
; ![]() - мольный поток реакционной смеси
на входе в реактор,
- мольный поток реакционной смеси
на входе в реактор, ![]() ;
; ![]() -
объемный поток реакционной смеси,
-
объемный поток реакционной смеси, ![]() .
.
Переходя к массовым концентрациям, получим уравнение
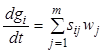 (7.42а)
(7.42а)
где независимая переменная ![]() есть отношение текущего объема реактора
и массового потока реакционной смеси:
есть отношение текущего объема реактора
и массового потока реакционной смеси:
![]() . (7.43а)
. (7.43а)
Если в качестве переменных используются удельные числа молей, то соответствующее уравнение имеет вид
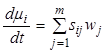 , (7.42б)
, (7.42б)
где независимая переменная ![]() является отношением текущего
объема реактора и мольного потока реакционной смеси на входе в аппарат:
является отношением текущего
объема реактора и мольного потока реакционной смеси на входе в аппарат:
![]() . (7.43б)
. (7.43б)
Если плотность и, следовательно, объемный поток смеси не меняются, то удобно перейти к объемным концентрациям
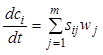 , (7.42в)
, (7.42в)
где независимая переменная ![]() есть отношение текущего объема реактора
и объемного потока реакционной среды:
есть отношение текущего объема реактора
и объемного потока реакционной среды:
![]() . (7.43в)
. (7.43в)
Независимую переменную ![]() , определяемую равенствами (7.43),
будем называть временем пребывания, хотя это название оправдано лишь для
равенства (7.43в). Для контактных каталитических реакторов при определенных
условиях справедливы аналогичные уравнения (см. ниже). Здесь переменную
, определяемую равенствами (7.43),
будем называть временем пребывания, хотя это название оправдано лишь для
равенства (7.43в). Для контактных каталитических реакторов при определенных
условиях справедливы аналогичные уравнения (см. ниже). Здесь переменную ![]() называют временем контакта.
называют временем контакта.
Уравнения (7.42) достаточно написать
лишь для ключевых компонентов, т. е. для ![]() ,
поскольку для остальных компонентов справедливы соответствующие
,
поскольку для остальных компонентов справедливы соответствующие
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.