Математические модели теплообменных процессов. Модель теплообменника с сосредоточенными параметрами. Модель теплообменника с распределенными параметрами

Здесь  - периметр теплопередающей поверхности в радиальном сечении теплообменника.

При рассмотрении условия стационарного режима теплообменника типа «труба в трубе» уравнения модели (6.6) можно преобразовать и представить в следующем виде:

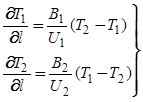.                                                    (6.7)

В противоточном теплообменнике температура по обеим сторонам трубы меняется по её длине. Если расходы греющего агента и нагреваемого продукта отличаются значительно (в несколько раз), то при выводе уравнений, приближенно описывающих тепловые процессы в теплообменниках, можно принять температуру на одной из сторон трубы постоянной (сторону малого расхода теплоносителя). Температуру на одной из сторон трубы можно принять постоянной в том случае, если на ней происходит конденсация чистого пара.

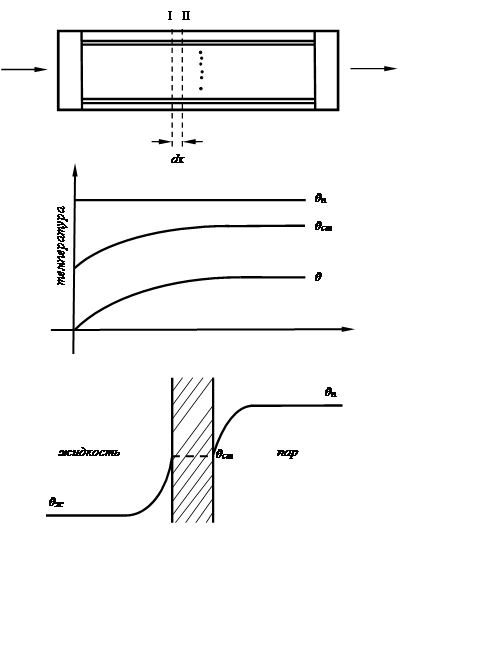
В качестве примера рассмотрим теплообменник (рис. 6.1), у которого по трубам протекает газ или жидкость, а на наружной поверхности труб происходит конденсация пара.

Рассмотрим характеристики теплообменника при изменении температуры пара от её значения в установившемся состоянии (возмущении по температуре пара). Выходной величиной является - отклонение температуры нагреваемой жидкости от её значения в установившемся состоянии.

Примем следующие допущения:

1.  Перенос тепла в оксиальном направлении отсутствует и параметры жидкости фактически постоянны.

2.  Для уменьшения порядка уравнения не будем учитывать ни термическое сопротивление стенки, ни тепловую емкость пленки конденсата.

Уравнение теплового баланса для потока жидкости на элементарном участке  трубы имеет вид:

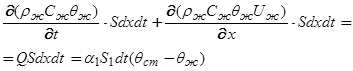,              (6.8)

где  - отклонение температуры от номинальных значений, отвечающих установившемуся  режиму.  - Сечение трубы,  - поверхность трубы, контактирующаяся с нагреваемой жидкостью на участке , - плотность жидкости, - теплоемкость жидкости,  - расстояние между сечениями I-II,  - промежуток времени,  - скорость движения жидкости,  - поток тепла в единице объема.

Первая составляющая определяет количество тепла, накопленное за промежуток времени  в элементе . Вторая составляющая определяет количество тепла, выведенного из сечения I–II за промежуток времени . Правая часть уравнения (6.8) есть количество тепла, переданное жидкости в сечении I-II от стенки трубы на участке  за время . Разделив правую и левую части уравнения (6.8) на ,получим:

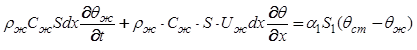.    (6.9)

Правую и левую часть уравнения (6.9) разделим на

.                       

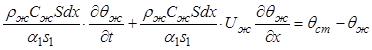Обозначив 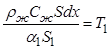, получим:

.                                          (6.10)

Уравнение теплового баланса для стенки:

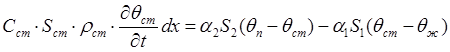,     или

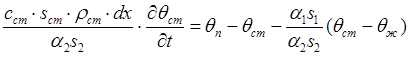,   (6.11)

где:  - поверхность теплообмена участка  со стороны греющего агента,  - площадь поперечного сечения стенки, ,  - коэффициенты теплоотдачи соответственно с внутренней и с наружной стороны трубы.

Обозначим:

, ,                                         

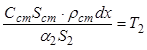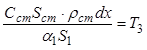Тогда:

.                                                                                

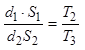Теперь: (6.11) можно записать в виде:

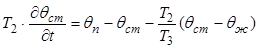.                                      (6.12)

Преобразуем (6.10) и (6.12) по Лапласу:

,                              (6.13)

.            (6.14)

Выразим  из (6.13)

.                                          

Подставив это выражение в (6.14), получим:

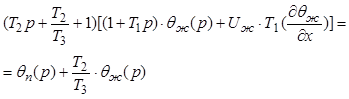.               (6.15)

После не сложных преобразований, вводя обозначения

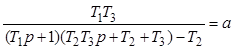,                                            6.16)

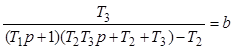,                                            (6.17)

Получим

.                                (6.18)

Рис. 6.1. Передача тепла в трубчатом теплообменнике

Решение уравнения (6.18) для граничного условия  при  представляет собой реакцию звена первого порядка на единичное ступенчатое возмущение  по величине :

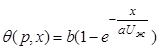,                                                              (6.19)

где величина  - время  прохождения жидкости через теплообменник, т.е. время запаздывания.

Передаточная функция теплообменника по каналу: изменение температуры пара - температура жидкости, полученная из уравнения (6.18) через его преобразование по Лапласу с аргументом :

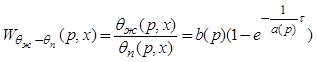.                       (6.20)

В отличие от объекта с сосредоточенными параметрами передаточная функция теплообменника с распределенными по длине трубы параметрами содержит член

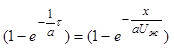.                                                           (6.21)

Если бы жидкость по трубе не перемещалась, то распределения температуры по длине трубы не наблюдалось бы. В выражении (6.20) этому факту отвечает , что приводит его к виду:

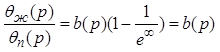.                                               (6.22)

В этом случае (6.22) принимает выражение (6.17) в виде передаточной функции динамического объекта второго порядка.

6.3. Модель погруженного теплообменника типа «смешение-вытеснение»

Погруженные теплообменники представляют собой трубчатый змеевик, погруженный в хладагент, непрерывно протекающий через емкость.

В тех случаях, когда в змеевике протекают реакции, зависящие от температуры, уравнение теплового баланса для змеевика составляют на основе гидродинамической модели идеального вытеснения, а для емкости - на основе модели идеального перемешивания. Учитывая все составляющие теплового баланса на основе уравнений (6.1) и (6.6), можно получить уравнения динамики теплообменника погруженного типа.

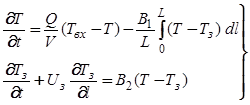,                                        (6.23)

где

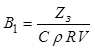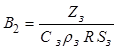, , .                                (6.24)

, ,  - входная температура, объемный расход теплоносителя и ее объем; ,  - сечение трубки змеевика и периметр сечения;  - суммарное термическое сопротивление; индекс «» - соответствует теплоносителю в змеевике.

Составляющие правой части первого части первого уравнения учитывают приток тепла с внешним потоком  и отвод его через стенку змеевика. Из-за распределенности змеевика для вычисления отводимого тепла