Описание нестационарной абсорбции в насадочной колонне. Структурная схема ячеечной модели с замкнутой цепью обменных процессов для нестанционного процесса

9.3.5. Описание нестационарной абсорбции в насадочной колонне

Рассмотренные ранее модели процесса абсорбции относились к стационарному случаю. В нестационарных условиях особую важность приобретает учет распределенности в пространстве и во времени основных гидродинамических параметров процесса: удерживающей способности, расхода жидкости в колонне, перепада давления. Многочисленными экспериментальными исследованиями было показано существование продольного перемешивания и застойных областей в насадочных абсорберах. В связи с этим модель абсорбера должна также отражать неравномерность распределения элементов потока в аппарате по времени пребывания и наличие взаимного обмена между газовой фазой, проточной зоной потока жидкости и застойной зоной потока жидкости с количественным выражением интенсивности обменных процессов.

Динамическая удерживающая способность абсорбера по жидкости , относительный объем застойных зон в системе и расход жидкости по колонне  в условиях нестационарного режима двухфазного потока в аппарате являются функциями времени  и координаты  в продольном направлении: , , где  - средняя скорость распространения вдоль колонны фронта гидродинамического возмущения; - площадь поперечного сечения аппарата.

Если принять, что продольное перемешивание в жидкой и газовой фазах характеризуются коэффициентами продольного перемешивания и , а скорость обмена веществом между газовой фазой и проточной зоной потока жидкости - коэффициентом , между проточной зоной и застойной зоной потока жидкости коэффициентом -  и между застойной зоной и газовой фазой - коэффициентом , то уравнения сохранения массы вещества в жидкой и газовой фазах запишутся в виде

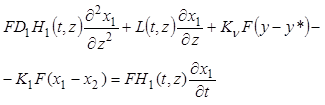,        (9.48)

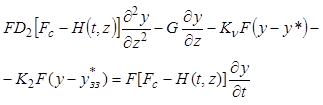.        (9.49)

Здесь x, у - соответственно концентрация передаваемого вещества в жидкости и газе;  - расход газа по колонне;  - свободный объем насадки; индексы 1 и 2 относятся к проточной и застойным зонам потока жидкости; - равновесный состав газа.

Уравнения (9.48), (9.49) должны быть дополнены уравнением, описывающим динамику распространения фронта гидродинамического возмущения в системе (возмущения по расходу жидкости):

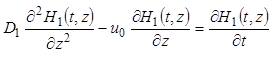                      (9.50)

и уравнением баланса массы для застойной зоны потока жидкости, обменивающейся веществом как с проточной зоной потока жидкости, так и с газовой фазой:

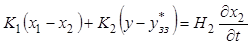.                          (9.51)

Если нестационарный процесс абсорбции протекает в стационарной гидродинамической обстановке, а источниками нестационарности служат только возмущения по составу потоков, то; следовательно,  и система уравнений (9.48) - (9.51) приводится к виду

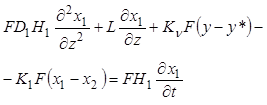,                      (9.52)

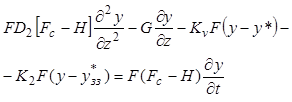,                (9.53)

.                           (9.54)

При условии полной стационарности процесса абсорбции

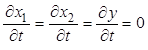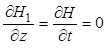; ; ;       (9.55)

и система уравнений (9.48) - (9.51) принимает обычный вид:

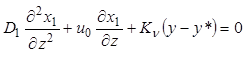,                            (9.56)

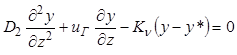.                              (9.57)

В уравнениях (9.48) - (9.51) . Таким образом, система (9.48) - (9.51) представляет собойзамкнутую систему уравнений относительно четырех неизвестных: концентрации растворенного

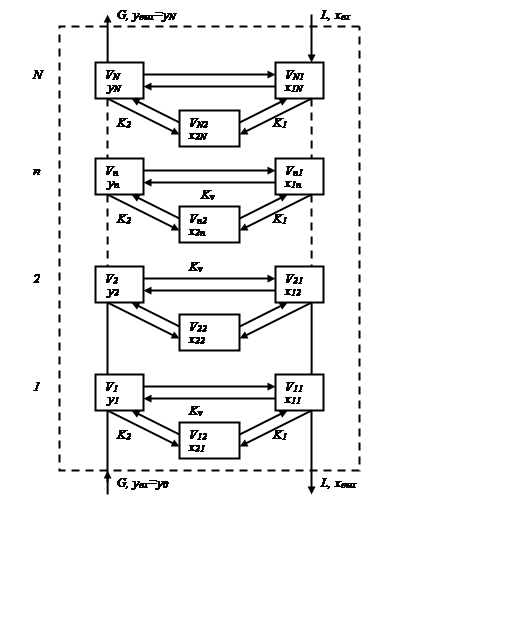Рис. 9.5. Структурная схема ячеечной модели с замкнутой цепью обменных процессов для нестанционного процесса абсорбции в насадочной колонне вещества в проточной части жидкой фазы , концентрации в застойной зоне аппарата , концентрации растворенного вещества в газовой фазе  и динамической удерживающей способности аппарата . Как видно из структуры системы (9.48) - (9.51), совместное решение ее уравнений сопряжено со значительными трудностями.. С точки зрения нахождения численных результатов удобнее перейти от системы (9.48) - (9.51) к эквивалентной симметричной ячеечной модели, учитывающей распределенность в пространстве и времени объемов ячеек:

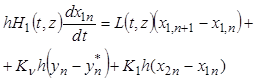,                         (9.58)

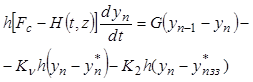,                          (9.59)

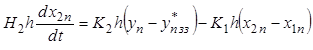,           (9.60)

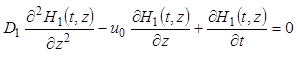.               (9.61)

Структурная схема ячеечной модели, отвечающая системе уравнений (9.58) - (9.61), представлена на рис. 9.5. Здесь ,  - концентрации растворенного вещества соответственно в проточной и застойной части -ой ячейки потока жидкости;  - концентрация в  -ой ячейке потока газа;  - переменный объем проточной части -ой ячейки потока жидкости;  - объем застойной части -ой ячейки потока жидкости  - переменный объем -ой ячейки потока газа; , ,  - коэффициенты массообмена замкнутой цепи обменных процессов между ячейками.

Отметим, что модель (9.58) - (9.61) включает как частный случай ячеечную модель. Так, если пренебречь распределенностью гидродинамических параметров по длине аппарата и во времени, а также влиянием застойной зоны, то система уравнений (9.58) - (9.61) сведется к нестационарной ячеечной модели:

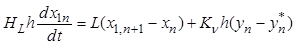,               (9.62) 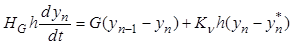. (9.63)

Система уравнений (9.58)-(9.61) представляет собой смешанную систему обыкновенных дифференциальных уравнений и уравнения с частными производными. Для решения этой системы удобно воспользоваться независимостью уравнения (9.61) от остальных уравнений. Решая это уравнение относительно искомой динамической удерживающей способности  для ступенчатого возмущения на  входе в аппарат, получаем

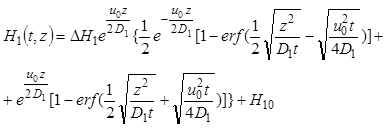.       (9.64)

В соответствии с дискретной природой ячеечной модели (9.58)-(9.61) следует перейти от непрерывного по времени и длине характера распределения (9.64) к дискретному по длине и непрерывному по времени распределению объемов ячеек:

, ,                                                     (9.65)

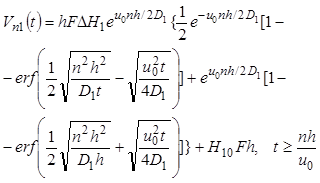,         (9.66)

где -высота колонны, соответствующая одной ячейке.

Выражения (9.65), (9.66) означают, что весь объем -ой ячейки непрерывно изменяется во времени, начиная с момента  поступления на эту ячейку фронта гидродинамического возмущения.

Помимо характера распределения объемов ячеек для расчета динамики процесса абсорбции в насадочном аппарате с помощью модели (9.58) - (9.61) необходимо знать величины входящих в нее параметров: числа ячеек, коэффициента массопередачи , а также коэффициентов обмена  и .

Исходя из граничных условий для аппарата конечных размеров число ячеек  симметричной ячеечной модели (число ячеек по газовой фазе равно числу ячеек по жидкой фазе) определяется выражением

.                                               (9.67)

Коэффициент обмена  между проточными и застойными зонами жидкости рассчитывается по следующей эмпирической зависимости:

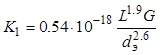.                                                 (9.68)

Коэффициент обмена  между газовой фазой и застойными зонами жидкости