Построение диаграммы фазового равновесия бинарной смеси
1. Содержание задания:
Постановка задачи:
При давлении P построить диаграмму фазового равновесия заданной 2-х компонентной смеси по моделям: а) идеальной смеси; б) Вильсона; в) NRTL.
Дано:
P, вещества.
Построить:
I график: T = f (xA); T = f (yA) – количество точек N = 101 смеси по моделям: а) идеальной смеси; б) Вильсона; в) NRTL.
II график: yA = f (xA) – количество точек N = 101. смеси по моделям: а) идеальной смеси; б) Вильсона; в) NRTL.
Варианты заданий:
|
Вариант |
Компоненты |
P |
Вариант |
Компоненты |
P |
||
|
1 |
1 |
2 |
2,6 |
26 |
2 |
3 |
1,4 |
|
2 |
2 |
3 |
0,6 |
27 |
3 |
1 |
2,6 |
|
3 |
3 |
1 |
3,0 |
28 |
1 |
2 |
3,3 |
|
4 |
1 |
2 |
3,8 |
29 |
2 |
3 |
0,9 |
|
5 |
2 |
3 |
3,7 |
30 |
3 |
1 |
5,0 |
|
6 |
3 |
1 |
1,9 |
31 |
1 |
2 |
5,5 |
|
7 |
1 |
2 |
3,4 |
32 |
2 |
3 |
4,3 |
|
8 |
2 |
3 |
3,6 |
33 |
3 |
1 |
4,3 |
|
9 |
3 |
1 |
1,9 |
34 |
1 |
2 |
4,3 |
|
10 |
1 |
2 |
2,0 |
35 |
2 |
3 |
1,7 |
|
11 |
2 |
3 |
0,7 |
36 |
3 |
1 |
4,4 |
|
12 |
3 |
1 |
1,2 |
37 |
1 |
2 |
5,3 |
|
13 |
1 |
2 |
4,0 |
38 |
2 |
3 |
2,1 |
|
14 |
2 |
3 |
1,2 |
39 |
3 |
1 |
4,9 |
|
15 |
3 |
1 |
2,0 |
40 |
1 |
2 |
4,2 |
|
16 |
1 |
2 |
2,6 |
41 |
2 |
3 |
2,5 |
|
17 |
2 |
3 |
3,2 |
42 |
3 |
1 |
2,9 |
|
18 |
3 |
1 |
3,1 |
43 |
1 |
2 |
2,8 |
|
19 |
1 |
2 |
5,4 |
44 |
2 |
3 |
3,2 |
|
20 |
2 |
3 |
4,3 |
45 |
3 |
1 |
3,2 |
|
21 |
3 |
1 |
3,4 |
46 |
1 |
2 |
4,6 |
|
22 |
1 |
2 |
5,1 |
47 |
2 |
3 |
5,1 |
|
23 |
2 |
3 |
2,7 |
48 |
3 |
1 |
1,5 |
|
24 |
3 |
1 |
1,3 |
49 |
1 |
2 |
2,1 |
|
25 |
1 |
2 |
1,4 |
50 |
2 |
3 |
2,5 |
Условные обозначения:
A – легколетучий компонент;
B – труднолетучий компонент;
xi – содержание i-го компонента в жидкой фазе,(мол.%);
yi – содержание i-го компонента в паровой фазе,(мол.%);
i – индекс компонента;
ki – константа фазового равновесия i-го компонента;
P – давление в системе, ата;
Pi – давление пара над чистым растворителем, ата;
T – температура системы, °С
Tкип i – температура кипения i-го компонента, °С
γ – коэффициент активности
Λij, Vi, λij – параметры модели Вильсона;
Gij, gij – параметры модели NRLT;
Математическая модель:
Стехиометрическое соотношение:
∑xi = 1; ∑yi = 1
Фазовое равновесие:
![]()
Константа фазового равновесия:
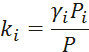
Давление насыщенных паров компонента i-го компонента:
![]()
Коэффициенты активности:
а) идеальная смесь
γ = 1
б) по Вильсону
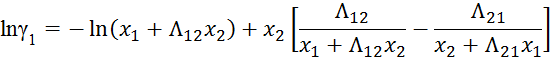
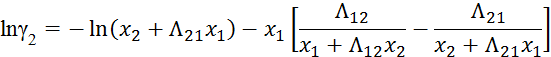
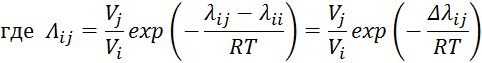
![]()
в) по NRLT
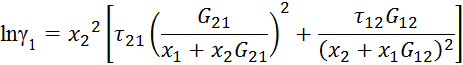
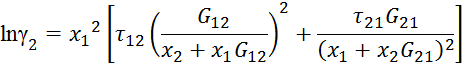
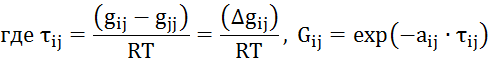
![]()
Примечание: верхний индекс – это квадрат.
Справочные данные:
Коэффициента уравнения Антуана
|
компонент |
Аi |
Вi |
Сi |
|
1 |
2,51 |
236,69 |
127,34 |
|
2 |
2,92 |
598,49 |
169,44 |
|
3 |
5,22 |
1742,00 |
234,00 |
Параметры энергетического взаимодействия молекул компонентов 1, 2, 3 для моделей Вильсона и NRLT:
|
∆λ12, ∆g12 |
∆λ13, ∆g13 |
∆λ21, ∆g21 |
∆λ23, ∆g23 |
∆λ31, ∆g31 |
∆λ32, ∆g32 |
|
-226,89 |
180,31 |
704,87 |
99,76 |
1722,10 |
1074,66 |
V1 = 104,00; V2 = 49,60; V3 = 18,70
a12 = 0,30; a13 = 0,20; a23 = 0,46
Алгоритм расчета по модели идеальной смеси:
1. Выписать коэффициенты Аi, Bi, Ci уравнения Антуана для заданной пары веществ.
2. Найти температуры кипения веществ согласно «алгоритму поиска температуры кипения Tкип при заданном давлении системы P» и определить из пары веществ легколетучее вещество А и тяжелолетучее вещество B.
3. Находим шаг по температуре
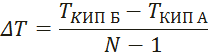
4. Находим Tj при j = 1, … , N.
T1 = TH Tj+1 = Tj + ΔT
5. Для каждой Tj находим PA и PB по уравнению Антуана.
6. Для каждой Tj находим KA и KB при γ = 1.
7. Для каждой Tj находим xA
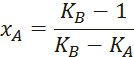
8. Для каждой Tj находим yA.
9. Строим графики.
Алгоритм расчета по моделям Вильсона и NRLT:
п. 1-7 те же, что в «алгоритме расчета по модели идеальной смеси»
8. Для x1 = xA и x2 = 1 – xA находим натуральные логарифмы коэффициентов активности lnγ1 и lnγ2 по модели Вильсона или NRLT.
9. Находим коэффициенты активности γ1 и γ2 по модели Вильсона или NRLT.
10. Для каждой Tj находим KA и KB при γ1 и γ2, рассчитанной в п.9.
11. Для каждой Tj уточняем xA
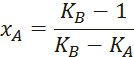
12. Для каждой Tj находим yA.
13. Строим графики.
Алгоритм поиска температуры кипения Tкип при давлении системы P:
1. Задать произвольную температуру T.
2. Найти Pi данного вещества при заданной температуре T по уравнению Антуана.
3. Если |Pi – P| < 0.001, то Tкип = T. Если |Pi – P| ≥ 0.001, то переходят к п.1, подбирая T до тех пор, пока не будет выполняться условие п.3.
2. Содержание отчета:
- постановка задачи
- цель работы
- ход выполнения работы, с описанием вычислений, результаты которых представить в виде графиков;
- выводы.
3. Вопросы для контроля:
1) Основные этапы построения математического описания массообменных процессов. На чем основывается математическое описание массообменного процесса?
2) Физический смысл диаграммы фазового равновесия. Гетерогенные и гомогенные системы. Зависимость диаграмм фазового равновесия от давления.
3) Фугитивность компонента в смеси, коэффициент активности компонента.
4) Уравнение Вильсона (концепция локальных составов). Уравнение NRTL (2 сорта ячеек).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.