а) система U,V, которая вращается с произвольной неизменной скоростью (wк=const);
б) система Х,Y, вращающаяся со скоростью вращения магнитного поля статора;
в) система d,q, вращающаяся со скоростью вращения ротора.
В качестве примера рассмотрим представление результирующего вектора в системе координат Х,Y.
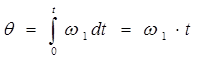 |
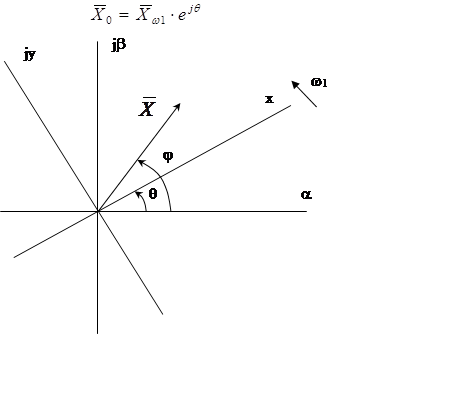 (2.3)
(2.3)
(2.4)
|
2.6 Баланс напряжений для статора.
С учетом принятых допущений уравнения напряжений для статорных обмоток можно записать следующим образом [6]:
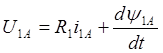 ,
,
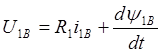 ,
,
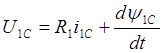 .
.
Здесь R1 – активное сопротивление фазных обмоток,y1А,В,С – потокосцепления обмоток.
После введения результирующих векторов система из трех уравнений преобразуется в одно уравнение:
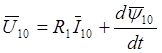 . (2.5)
. (2.5)
Здесь индекс «0» учитывает запись уравнения в неподвижной системе координат.
Учитывая, что ![]() ,
, ![]() ,
, ![]() получим разложение
уравнения (5) по осям a,b:
получим разложение
уравнения (5) по осям a,b:
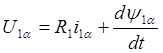 , (2.6)
, (2.6)
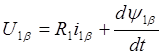 .
.
Для нахождения уравнений, описывающих переходные процессы во вращающейся системе координат используем соотношение (2.4). Тогда
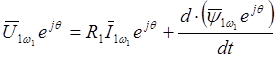 . (2.7)
. (2.7)
Применяя правило дифференцирования сложной функции, находим:
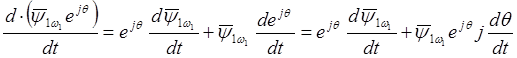
Так как 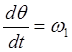 , то после подстановки
вычисленной производной в (2.7) и сокращая на еjq будем иметь:
, то после подстановки
вычисленной производной в (2.7) и сокращая на еjq будем иметь:
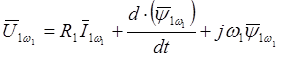 . (2.8)
. (2.8)
Раскладывая результирующие векторы на составляющие по осям Х и Y, запишем:
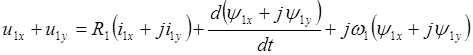 .
.
Следовательно,
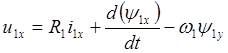 , (2.9)
, (2.9)
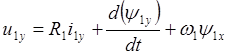 .
.
Обобщая результат для системы координат, вращающейся с произвольной скоростью wк=const, можем записать:
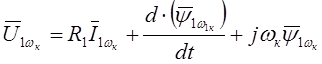 (2.10)
(2.10)
2.7 Баланс напряжений для ротора.
В общем случае асинхронный двигатель может потреблять энергию не только со стороны статора, но и со стороны ротора (машина двойного питания). При этом электромагнитные процессы в роторе описываются уравнениями:
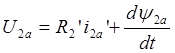 ,
,
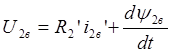 ,
,
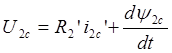 .
.
При отсутствии питания со стороны ротора U2а=U2в=U2с=0.
Приведенные уравнения записаны в системе координат, четко связанной с ротором (система d,q). Для обозначения результирующих векторов напряжения, тока, и потокосцепления в этом случае используем индекс «w». Тогда:
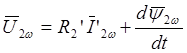 . (2.11)
. (2.11)
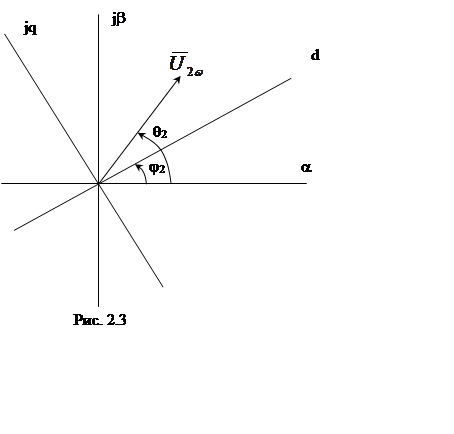
Если вектор повернут относительно системы координат a,b на угол q2 (рис. 2.3), то согласно (2.3), (2.4)
![]() ,
, ![]() .
.
 |
Аналогичными соотношениями описываются и другие результирующие векторы. Тогда:
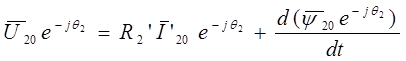 .
.
Учитывая, что 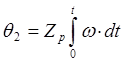 , где Zp – число пар полюсов, после вычисления производной и сокращения и
правой, и левой частей уравнения на е-jq2, получим:
, где Zp – число пар полюсов, после вычисления производной и сокращения и
правой, и левой частей уравнения на е-jq2, получим:
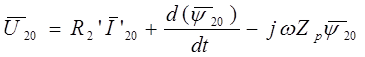 . (2.12)
. (2.12)
После разложения уравнения (2.12) по осям a и b имеем:
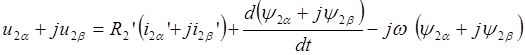 ,
,
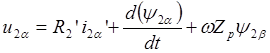 ,
(2.13)
,
(2.13)
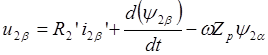 .
.
Используя соотношение(2.4), уравнение (2.12) преобразуем к виду
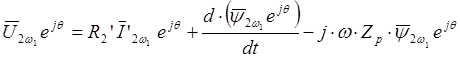 .
.
С учетом выражения (2.8) получим:
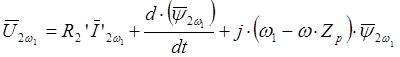 . (2.14)
. (2.14)
Разложение результирующих векторов по осям Х и Y дает следующий результат:
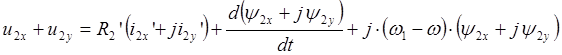 ,
,
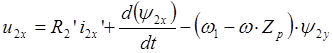 , (2.15)
, (2.15)
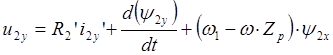 .
.
Обобщая результат для системы координат, вращающейся с произвольной скоростью wк=const, баланс напряжений в роторной цепи можно представить в следующем виде:
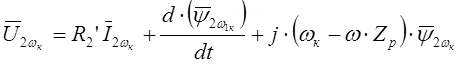 .
(2.16)
.
(2.16)
2.8 Потокосцепления.
Потокосцепление y1А фазы А обмотки статора создается совместным действием токов статора и ротора всех фаз.
Составляющая потокосцепления y1А, создаваемая токами статора, равна:
![]() .
.
Здесь L0 – индуктивность обмотки статора, обусловленная основным потоком; L1g - индуктивность обмотки статора, обусловленная потоком рассеяния; М – взаимоиндуктивность между обмотками статора.
Так как i1В+i1С=-i1А, то ![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.